Szilassi Polyhedron

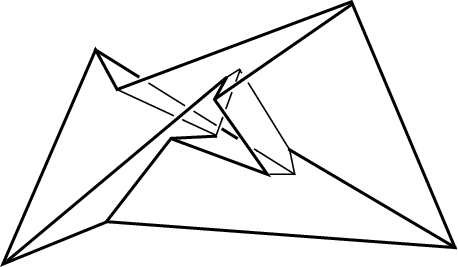
$\begin{figure}\begin{center}\BoxedEPSF{szilassi_polyhedron.epsf scaled 900}\end{center}\end{figure}$

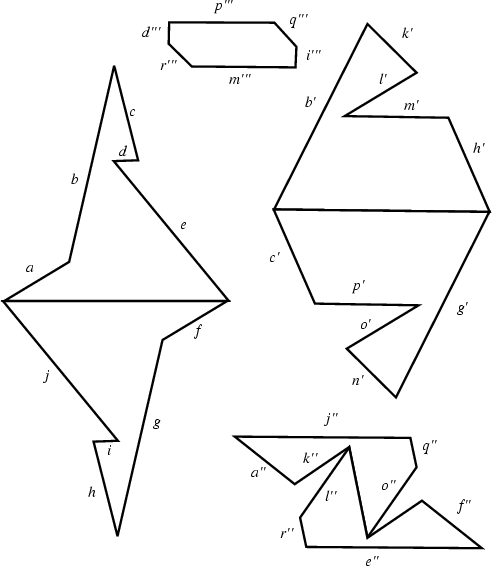
$\begin{figure}\begin{center}\BoxedEPSF{SzilassiPolyhedronNet.epsf scaled 800}\end{center}\end{figure}$

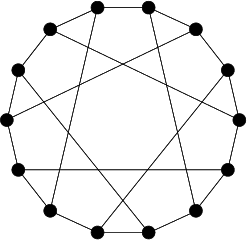
A Polyhedron which is topologically equivalent to a Torus and for which every pair of faces has an Edge in common. This polyhedron was discovered by L. Szilassi in 1977. Its Skeleton is equivalent to the seven-color torus map illustrated below.

$\begin{figure}\begin{center}\BoxedEPSF{szilassi_Polyhedron_Map.epsf scaled 800}\end{center}\end{figure}$

The Szilassi polyhedron has 14 Vertices, seven faces, and 21 Edges, and is the Dual Polyhedron of the Császár Polyhedron.

References

Eppstein, D. ``Polyhedra and Polytopes.'' http://www.ics.uci.edu/~eppstein/junkyard/polytope.html.

Gardner, M. Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. New York: W. H. Freeman, pp. 118-120, 1992.

Hart, G. ``Toroidal Polyhedra.'' http://www.li.net/~george/virtual-polyhedra/toroidal.html.