|
|
|
A Recursive Function devised by I. Takeuchi. For Integers ![]() ,
, ![]() , and
, and ![]() , and a
function
, and a
function ![]() , it is
, it is
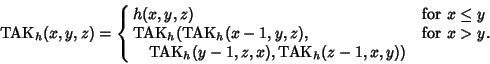
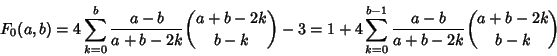
The TAK function is also connected with the Ballot Problem (Vardi 1991).
See also Ackermann Function, Ballot Problem
References
Gabriel, R. P. Performance and Implementation of Lisp Systems. Cambridge, MA: MIT Press, 1985.
Knuth, D. E. Textbook Examples of Recursion. Preprint 1990.
Vardi, I. ``The Running Time of TAK.'' Ch. 9 in Computational Recreations in Mathematica.
Redwood City, CA: Addison-Wesley, pp. 179-199, 1991.