|
|
|
Also known as Ramanujan's Hypothesis. Ramanujan ![]() proposed that
proposed that
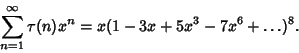
See also Tau Function
References
Deligne, P. ``La conjecture de Weil. I.'' Inst. Hautes Études Sci. Publ. Math. 43, 273-307, 1974.
Deligne, P. ``La conjecture de Weil. II.'' Inst. Hautes Études Sci. Publ. Math. 52, 137-252, 1980.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 169,
1959.