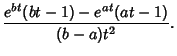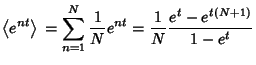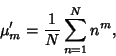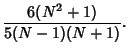A distribution which has constant probability is called a uniform distribution, sometimes also called a
Rectangular Distribution. The probability density function and cumulative distribution function for a
continuous uniform distribution are
With  and
and 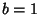 , these can be written
, these can be written
The Characteristic Function is
 |
(5) |
where
The Moment-Generating Function is
![\begin{displaymath}
M(t)=\left\langle{e^{xt}}\right\rangle{} =\int_a^b {e^{xt}\over b-a} dx=\left[{e^{xt}\over t(b-a)}\right]_a^b,
\end{displaymath}](u_181.gif) |
(8) |
so
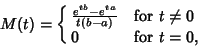 |
(9) |
and
The function is not differentiable at zero, so the Moments cannot be found using the standard technique. They can,
however, be found by direct integration. The Moments about 0 are
The Moments about the Mean are
so the Mean, Variance, Skewness, and Kurtosis are
The probability distribution function and cumulative distributions function for a discrete uniform
distribution are
for 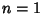 , ...,
, ...,  . The Moment-Generating Function is
. The Moment-Generating Function is
The Moments about 0 are
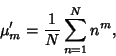 |
(26) |
so
and the Moments about the Mean are
The Mean, Variance, Skewness, and Kurtosis are
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 531 and 533, 1987.
© 1996-9 Eric W. Weisstein
1999-05-26
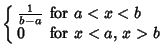
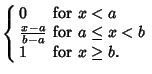
![\begin{displaymath}
M(t)=\left\langle{e^{xt}}\right\rangle{} =\int_a^b {e^{xt}\over b-a} dx=\left[{e^{xt}\over t(b-a)}\right]_a^b,
\end{displaymath}](u_181.gif)
![$\displaystyle {1\over b-a}\left[{{1\over t}(be^{bt}-ae^{at})-{1\over t^2}(e^{bt}-e^{at})}\right]$](u_184.gif)