Consider the differential equation satisfied by
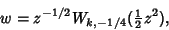 |
(1) |
where 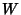 is a Whittaker Function.
is a Whittaker Function.
![\begin{displaymath}
{d\over z\,dz}\left[{d(wz^{1/2})\over z\,dz}\right]+\left({-{1\over 4}+{2k\over z^2} +{3\over 4z^4}}\right)wz^{1/2}=0
\end{displaymath}](w_377.gif) |
(2) |
 |
(3) |
This is usually rewritten
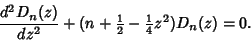 |
(4) |
The solutions are Parabolic Cylinder Functions.
The equations
 |
(5) |
 |
(6) |
which arise by separating variables in Laplace's Equation in Parabolic Cylindrical Coordinates, are also
known as the Weber differential equations. As above, the solutions are known as Parabolic Cylinder Functions.
© 1996-9 Eric W. Weisstein
1999-05-26