An antisymmetric operation on Differential Forms (also called the Exterior Derivative)
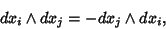 |
(1) |
which Implies
The wedge product is Associative
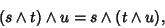 |
(6) |
and Bilinear
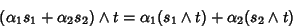 |
(7) |
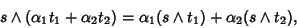 |
(8) |
but not (in general) Commutative
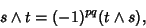 |
(9) |
where 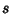 is a
is a 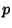 -form and
-form and 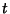 is a
is a 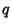 -form. For a 0-form
-form. For a 0-form 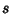 and 1-form
and 1-form 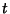 ,
,
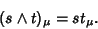 |
(10) |
For a 1-form 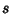 and 1-form
and 1-form 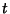 ,
,
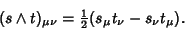 |
(11) |
The wedge product is the ``correct'' type of product to use in computing a Volume Element
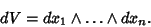 |
(12) |
See also Differential Form, Exterior Derivative, Inner Product, Volume Element
© 1996-9 Eric W. Weisstein
1999-05-26