|
|
|
The Quasiperiodic Function defined by
| (1) |
| (2) |
![$\displaystyle -\int_0^z [\wp(z)-z^{-2}]\,dz$](w_671.gif) |
|||
![$\displaystyle -\Sigma'\int_0^z [(z-\Omega_{mn})^{-2}-\Omega_{mn}^{-2}]\,dz$](w_672.gif) |
(3) |
![\begin{displaymath}
\zeta(z)=z^{-1} + \setbox0=\hbox{$\scriptstyle{m,n =-\infty}...
...fty [(z-\Omega_{mn})^{-1}+\Omega_{mn}^{-1} +z\Omega_{mn}^{-2}]
\end{displaymath}](w_673.gif) |
(4) |
| (5) |
| (6) |
If ![]() , then
, then
| (7) |
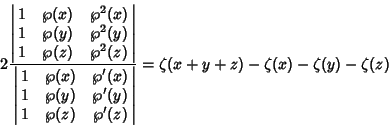 |
(8) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Weierstrass Elliptic and Related Functions.'' Ch. 18 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 627-671, 1972.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.