N.B. A detailed on-line essay by S. Finch
was the starting point for this entry.
Let a piecewise smooth function 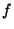 with only finitely many discontinuities (which are all jumps) be defined on
with only finitely many discontinuities (which are all jumps) be defined on ![$[-\pi,
\pi]$](w_968.gif) with Fourier Series
with Fourier Series
![\begin{displaymath}
S_n(f,x)={\textstyle{1\over 2}}a_0+\left\{{\sum_{k=1}^n [a_k\cos(kx)+b_k\sin(kx)]}\right\}.
\end{displaymath}](w_973.gif) |
(3) |
Let a discontinuity be at 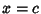 , with
, with
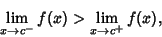 |
(4) |
so
![\begin{displaymath}
D\equiv \left[{\,\lim_{x\to c^-} f(x)}\right]-\left[{\,\lim_{x\to c^+} f(x)}\right]>0.
\end{displaymath}](w_976.gif) |
(5) |
Define
![\begin{displaymath}
\phi(c)={1\over 2} \left[{\,\lim_{x\to c^-} f(x)+\lim_{x\to c^+} f(x)}\right],
\end{displaymath}](w_977.gif) |
(6) |
and let 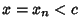 be the first local minimum and
be the first local minimum and 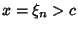 the first local maximum of
the first local maximum of 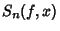 on either side of
on either side of
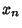 . Then
. Then
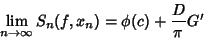 |
(7) |
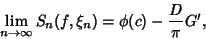 |
(8) |
where
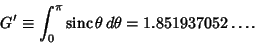 |
(9) |
Here,
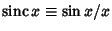 is the Sinc Function. The Fourier Series of
is the Sinc Function. The Fourier Series of 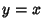 therefore does not
converge to
therefore does not
converge to 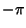 and
and 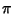 at the ends, but to
at the ends, but to 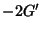 and
and 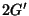 . This phenomenon was observed by Wilbraham (1848) and
Gibbs (1899). Although Wilbraham was the first to note the phenomenon, the constant
. This phenomenon was observed by Wilbraham (1848) and
Gibbs (1899). Although Wilbraham was the first to note the phenomenon, the constant 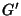 is frequently (and unfairly)
credited to Gibbs and known as the Gibbs Constant. A related constant sometimes also called the Gibbs
Constant is
is frequently (and unfairly)
credited to Gibbs and known as the Gibbs Constant. A related constant sometimes also called the Gibbs
Constant is
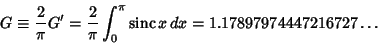 |
(10) |
(Le Lionnais 1983).
References
Carslaw, H. S. Introduction to the Theory of Fourier's Series and Integrals, 3rd ed. New York: Dover, 1930.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/gibbs/gibbs.html
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 36 and 43, 1983.
Zygmund, A. G. Trigonometric Series 1, 2nd ed. Cambridge, England: Cambridge University Press, 1959.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() with only finitely many discontinuities (which are all jumps) be defined on
with only finitely many discontinuities (which are all jumps) be defined on ![]() with Fourier Series
with Fourier Series
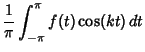
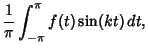
![\begin{displaymath}
S_n(f,x)={\textstyle{1\over 2}}a_0+\left\{{\sum_{k=1}^n [a_k\cos(kx)+b_k\sin(kx)]}\right\}.
\end{displaymath}](w_973.gif)