一、完全随机设计的多个样本均数的比较
又称单因素方差分析。把总变异分解为组间(处理间)变异和组内变异(误差)两部分。目的是推断k个样本所分别代表的μ1,μ2,……μk是否相等,以便比较多个处理的差别有无统计学意义。其计算公式见表19-6。
表19-6 完全随机设计的多个样本均数比较的方差分析公式
| 变异来源 | 离均差平方和SS | 自由度v | 均方MS | F |
| 总 | ΣX2-C* | N-1 | ||
| 组间(处理组间) | 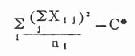 | k-1 | SS组间/v组间 | MS组间/MS组间 |
| 组内(误差) | SS总-SS组间 | N-k | SS组内/v组内 |
*C=(ΣX)2/N=Σni,k为处理组数
表19-7 F值、P值与统计结论
| α | F值 | P值 | 统计结论 |
| 0.05 | <F0.05(v1.V2) | >0.05 | 不拒绝H0,差别无统计学意义 |
| 0.05 | ≥F0.05(v1.V2) | ≤0.05 | 拒绝H0,接受H1,差别有统计学意义 |
| 0.01 | ≥F0.01(v1.V2) | ≤0.01 | 拒绝H0,接受H1,差别有高度统计学意义 |
方差分析计算的统计量为F,按表19-7所示关系作判断。
例19.9 某湖水不同季节氯化物含量测量值如表19-8,问不同季节氯化物含量有无差别?
表19-8 某湖水不同季节氯化物含量(mg/L)
| Xij | 春 | 夏 | 秋 | 冬 | |||||
| 22.6 | 19.1 | 18.9 | 19.0 | ||||||
| 22.8 | 22.8 | 13.6 | 16.9 | ||||||
| 21.0 | 24.5 | 17.2 | 17.6 | ||||||
| 16.9 | 18.0 | 15.1 | 14.8 | ||||||
| 20.0 | 15.2 | 16.6 | 13.1 | ||||||
| 21.9 | 18.4 | 14.2 | 16.9 | ||||||
| 21.5 | 20.1 | 16.7 | 16.2 | ||||||
| 21.2 | 21.2 | 19.6 | 14.8 | ||||||
| ΣXijj | 167.9 | 159.3 | 131.9 | 129.3 | 588.4(ΣX) | ||||
| ni | 8 | 8 | 8 | 8 | 32(N) | ||||
| Xi | 20.99 | 19.91 | 16.49 | 16.16 | |||||
| ΣX2ijj | 3548.51 | 3231.95 | 2206.27 | 2114.11 | 11100.84(ΣX2) | ||||
H0:湖水四个季节氯化物含量的总体均数相等,即μ1=μ2=μ3=μ4
H1:四个总体均数不等或不全相等
α=0.05
先作表19-8下半部分的基础计算。
C= (Σx)2/N=(588.4)2/32=10819.205
SS总=Σx2-C=11100.84-10819.205=281.635
V总=N-1=31

V组间=k-1=4-1=3
SS组内=SS总-SS组间=281.635-141.107=140.465
V组内=N-k=32-4=28
MS组间=SS组间/v组间=141.107/3=47.057
MS组内=SS组内/v组内=140.465/28=5.017
F=MS组间/MS组内=47.057/5.017=9.380
以v1(即组间自由度)=3,v2(即组内自由度)=28查附表19-2,F界值表,得F0.05(3,28)=2.95,F0.01(3,28)=4.57。本例算得的F=9.380>F0.01(3,28),P<0.01,按α=0.05检验水准拒绝H0,接受H1,可认为湖水不同季节的氯化物含量不等或不全相等。必要时可进一步和两两比较的q检验,以确定是否任两总体均数间不等。
资料分析时,常把上述计算结果列入方差分析表内,如表19-9。
表19-9 例19.9资料的方差分析表
| 变异来源 | SS | v | MS | F | P |
| 组间 | 141.170 | 3 | 47.057 | 9.38 | <0.01 |
| 组内 | 140.465 | 28 | 5.017 | ||
| 总 | 281.635 | 31 |
| 上一页:第四节 方差分析 |
| 当前页:一、完全随机设计的多个样本均数的比较 |
| 下一页:二、随机区组(配伍组)设计的多个样本均数比较 |