二、随机区组(配伍组)设计的多个样本均数比较
又称两因素方差分析。把总变异分解为处理间变异、区组间变异及误差三部分。除推断k个样本所代表的总体均数,μ1,μ2,……μk是否相等外,还要推断b个区组所代表的总体均数是否相等。也就是说,除比较多个处理的差别有无统计学意义外,还要比较区组间的差别有无统计学意义。该设计考虑了个体变异对处理的影响,故可提高检验效率。
表19-10随机区组设计的多个样本均数比较的方差分析公式
| 变异来源 | 离均差平方和SS | 自由度v | 均方MS | F |
| 总 | ΣX2-C | N-1 | ||
| 处理间 | 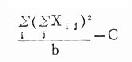 | k-1 | SS处理/v处理 | MS处理/MS误差 |
| 区组间 | 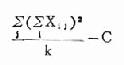 | b-1 | SS区组/v区组 | MS区组MS误差 |
| 误差 | SS总-SS处理-SS区组 | V总-v处理-v区组 | SS误差/v误差 |
C、k、N的意义同表19-6,b为区组数
例19.10为研究酵解作用对血糖浓度的影响,从8名健康人中抽血并制成血滤液。每个受试者的血滤液被分成4份,再随机地把4份血滤液分别放置0,45,90,135分钟,测定其血溏浓度(表19-11),试问放置不同时间的血糖浓度有无差别?
处理间:
H0:四个不同时间血糖浓度的总体均数相等,即μ1=μ2=μ3=μ4
表19-11 血滤放置不同时间的血糖浓度(mmol/L)
| 区组号 | 放置时间(分) | 受试者小计 ΣXij j | |||
| 0 | 45 | 90 | 135 | ||
| 1 | 5.27 | 5.27 | 4.94 | 4.61 | 20.09 |
| 2 | 5.27 | 5.22 | 4.88 | 4.66 | 20.03 |
| 3 | 5.88 | 5.83 | 5.38 | 5.00 | 22.09 |
| 4 | 5.44 | 5.38 | 5.27 | 5.00 | 21.09 |
| 5 | 5.66 | 5.44 | 5.38 | 4.88 | 21.36 |
| 6 | 6.22 | 6.22 | 5.61 | 5.22 | 23.27 |
| 7 | 5.83 | 5.72 | 5.38 | 4.88 | 21.81 |
| 8 | 5.27 | 5.11 | 5.00 | 4.44 | 19.82 |
| ΣXij j | 44.84 | 44.19 | 41.84 | 38.69 | 169.56(ΣX) |
| Ni | 8 | 8 | 8 | 8 | 32(N) |
| Xi | 5.6050 | 5.5238 | 5.2300 | 4.8363 | |
| ΣX2ij j | 252.1996 | 245.0671 | 219.2962 | 187.5585 | 904.1214(ΣX2) |
H1:四个总体均数不等或不全相等
α=0.05
区组间:
H0:八个区组的总体均数相等,即μ1=μ2=……μ8
H1:八个区组的总体均数不等或不全相等
α=0.05
先作表19-11下半部分和右侧一栏的基本计算。
C=(ΣX)2/N=(169.56)2/32=898.45605
SS总=ΣX2-C=904.1214-898.45605=5.66535
V总=N-1=32-1=31
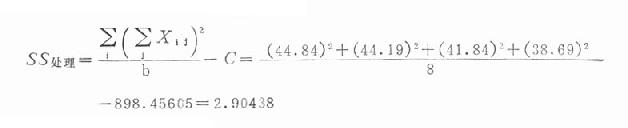
V处理=k-1=4-1=3
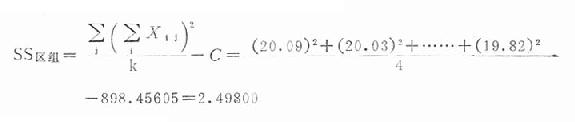
V区组=b-1=8-1=7
SS误差=SS总-SS处理-SS区组=5.66535-2.90438-2.49800=0.26297
V误差=(k-1)(b-1)=3×7=21
MS处理=SS处理/v处理=2.90438/3=0.9681
MS区组=SS区组/v区组=2.49800/7=0.3569
MS误差=SS误差/v误差=0.26297/21=0.0125
F处理=MS处理/MS误差=0.9681/0.0125=77.448
F区组=MS区组/MS误差=0.3569/0.0125=28.552
推断处理间的差别,按v1=3,v2=21查F界值表,得F0.005(3,21)=3.07,F0.01(3,21)=4.87,P<0.01;推断区组间的差别,按v1=7,v2=21查F界值表,得F0.05(7,21)=2.49,F0.01(7,21)=3.64,P<0.01。按α=0.05检验水准皆拒绝H0,接受H1,可认为放置时间长短会影响血糖浓度且不同受试者的血糖浓度亦有差别。但尚不能认为任两个不同放置时间的血糖浓度总体均数皆有差别,必要时可进一步作两两比较的q检验。
表19-12 例19.10资料的方差分析表
| 变异来源 | SS | v | MS | F | P |
| 处理间 | 2.90438 | 3 | 0.9681 | 77.448 | <0.01 |
| 区组间 | 2.49800 | 7 | 0.3569 | 28.552 | <0.01 |
| 误差 | 0.26297 | 21 | 0.0125 | ||
| 总 | 5.66538 | 31 |
| 上一页:一、完全随机设计的多个样本均数的比较 |
| 当前页:二、随机区组(配伍组)设计的多个样本均数比较 |
| 下一页:三、多个样本均数间的两两比较的q检验 |