一、检验的一般步骤
1.资料 这里所要的是类似第七章第一节三、中所述的成组资料,不过现在不是两组而是多组,如下例。
例8.1 分泌型免疫球蛋白A(SIgA)是胃肠道分泌液、泪液等外分泌液中的主要免疫球蛋白类,某院研制了“125I-SIgA放射免疫测定药盒”,为人体SIgA的检验提供了一种简便方法。为比较不同批号药盒检验结果是否一致,该院曾将三批号各四个药盒一一测定了某一标本得结果如下,试作方差分析。
表8.1 三个批号药盒的SIgA放射免疫测定值
| 批号 | SIgA含量(μg/ml), X | ∑X | n | X | ∑X2 | ∑X2-(∑X)2/n | |||
| 1 | 1.92 | 1.80 | 2.08 | 2.00 | 7.80 | 4 | 1.95 | 15.2528 | 0.0428 |
| 2 | 2.21 | 2.25 | 2.12 | 2.57 | 9.15 | 4 | 2.29 | 21.0459 | 0.1153 |
| 3 | 3.27 | 2.75 | 2.90 | 3.10 | 12.02 | 4 | 3.01 | 36.2754 | 0.1553 |
| 合计 | 28.97 | 12 | 2.414 | 72.5741 | 0.3134 | ||||
2. 分析 从表8.1的测定结果可以看出这里有三种变异:
(1)从同一批号药盒的四次测定结果看,不尽相同,这是组内变异。显然它不是由于批号不同的影响,而只是由于误差(如批内各药盒的差异性和测量误差等)造成的。
(2)从各批测定值的均数来看,是不相同的,这是组间变异,表明各批药盒性能质量也许对测得的结果有一定影响,也包括误差的作用。
(3)12次测定的SIgA含量都不尽相同,有高有低,它们既可能受药盒来自不同批号的影响,也包括组内变异,因此称为总变异。
那么这里各批药盒测SIgA均值间的差别,只不过是抽样误差的反映呢?还是药盒制作质量不稳定,批间存在显著差别?为了得出正确的结论,可进行方差分析。方差分析的基本甲思想是:①从总变异中分出组间变异和组内变异,并用数量表示变异的程度;②将组间变异和组内变异进行比较,如两者相差不大,说明受批号不同的影响不大;如果两者相差较大,组间变异比组内变异大得多,说明批号不同的影响不容忽视。下面我们根据表8.1资料来计算这三种变异。
(1)总离均差平方和:即12个观察值各与总均数相差的平方之和,公式为
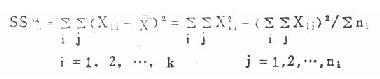
式中SS总即总离均差平方和,Xij表示第i组的第j个观察值,X为全部观察值的平均数,k是组数。
本例SS总=72.5741-28.972/12=2.6357
(2)组间离均差平方和:即取各组均数代替该组各观察值后,它们分别与总均数相差的平方之和,公式为
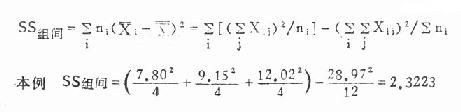
(3)组内离均差平方和:只要加总各组本身的离均差平方和即得,公式为
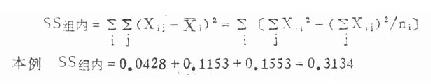
由本例计算结果可以看出,SS组间+SS组内=SS总,如2.3223+0.3134=2.6357。因此,算出SS总以后再计算SS组间、SS组内两者中之一个,其余一个便可通过减法求得。
将以上求得的几种变异各除以自由度后得均方。自由度的计算公式分别为
总变异 N-1 (N为各组例数之和)( 8.4)
组间变异 K-1 (8.5)
组内变异 N-K (8.6)
组间均方与组内均方之比为F值,
F=组间均方/组内均方 (8.7)
本例
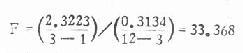
将以上数据列入下面的方差分析表可使人一目了然。
表8.2 方差分析表
| 变异来源 | 离均差平方和 | 自由度 | 均 方 | F |
| 总 变 异 | 2.6357 | 11 | ||
| 组间变异 | 2.3223 | 2 | 1.1612 | 33.368 |
| 组内变异 | 0.3134 | 9 | 0.0348 |
如果求得的F值小于1或略大于1,也即组间变异与组内变异差不多,则关于不同批药盒所致影响就不值得注意,反之,若各批均数间差别甚大,组间变异比组内变异大得多,说明不能只把它看成为误差的表面,很可能不同批药盒的测定值具有差别。现F值远大于1,若等于或大于某α水准下的临界F值,便将拒绝检验假设H0而接受备择假设H1。
本例定α=0.05,查附表8F值表,F0.05(2,9)=4.26。括弧内2为求F值时分子(也即较大均方)的自由度,9为分母的自由度,今F=33.368,远大于此临界值4.26,故P<0.05,说明不同批药盒的影响不容忽视,各批药盒测定的SIgA值相差显著。
| 上一页:第一节 方差分析的意义 |
| 当前页:一、检验的一般步骤 |
| 下一页:二、多个均数间的两两比较 |