二、多个均数间的两两比较
经方差分析(即F检验),若各组均数之间差别不显着,则到此为止,不必作进一步统计学处理了。当F检验结果为相差显着时,这只是对各组均数的整体而言,至于哪些均数间的差别显着,哪些不显着,还要作如下进一步分析。
本例检验结果为相差显着,这里我们先用较为简单而实用的最小显着差数法来比较三组中每两组均数间的差别是否显着,然后介绍q值法。
1.最小显着差数法
(1)计算最小显着性差数Dα,ν
Dα,ν=t, 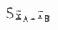
式中t,由附表3查得,查时自由度ν用方差分析表中组内变异的自由度,本例为9;α即显著性水准,常用0.05或0.01,本例查得两个临界t值即t0.05,9=2.262,t0.01,9=3.250。标准误 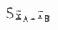
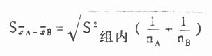
S2组内也即表8.2中的组内均方(也可叫误差均方)0.0348。nA、nB为所比较的两组的例数,本例各组例数都为4。现将数据代入式(8.9)、(8.8)求得
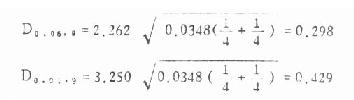
(2)用上述的最小显著性差数与每两组均数的相差数比,若后者大于前者(临界值),便相差显著,若小于前者,为相差不显著。现将两均数间的比较结果列于下表。
表8.3 均数间两两比较
| A与B(批号) | ∣XA-XB∣ | 界 值 | P值 | |
| D0.05 | D0.01 | |||
| 1与2 | 0.34 | 0.298 | 0.429 | <0.05 |
| 1与3 | 1.06 | 0.298 | 0.429 | <0.01 |
| 2与3 | 0.72 | 0.298 | 0.429 | <0.01 |
注:表中XA-XB两侧的直杠是绝对值符号。
3.统计结论:各批间均在α=0.05水准处相差显著,又第3批与第1、2两批比,P<0.01,说明各批药盒对SIgA的检测效果不一致,批号3远高于批号2与1。
上面介绍的多个均数间两两比较的方法虽较简便,精确性有时不足,尤其当比较的均数不是在三个而是更多,或各样本含量不相等时应用也较麻烦。下面介绍查临界q值而不查t值的另一比较方法。
2.q值法
(1)将表8.1中三个均数自大至小排列得:
| 第3批 | 第2批 | 第1批 | |
| SIgA平均值,X(μg/ml) | 3.01 | 2.29 | 1.95 |
| 秩次 | 1 | 2 | 3 |
| 样本含量,n | 4 | 4 | 4 |
(2)用组内均方与平均每组例数n0求出标准误,然后与由附表9中查到的临界q值相乘,即可列出比较表加以比较。下面是求平均例数的公式。
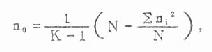
此例
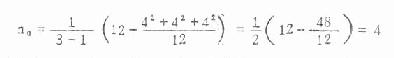
本例各组样本大小相等,均为4,本无须用上式计算,但若各组大小不等时就得用上式求平均例数。
标准误公式为
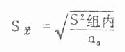
此例
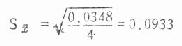
表8.4 均数间两两比较
| A与B (秩次) | 组数α | ∣XA-XB∣ | Q0.05(a,ν)Sχ | ν见组内变异一行 P值 |
| 3与2 | 2 | 0.34 | 0.299 | <0.05 |
| 3与1 | 3 | 1.06 | 0.369 | <0.05 |
| 2与1 | 2 | 0.72 | 0.299 | <0.05 |
现将上表栏目自左至右一一说明如下:
表内左侧,均数大小秩次3与2比,即相邻两组相比,故组数a等于2。同样,第三行的2与1比,因2与1相邻,a也是2,3与1比则由3到1组数有3,a等于3。关于查附表9中的q值,一方面根据该表上端横行a的数字,另方面根据表左侧直行的ν,也即方差分析表中组内(或误差)项的自由度(本例为9)来查。表内q值有上、下两行数,若定α为0.05,查上行,α为0.01则查下行。
就本例言,用两种方法作均数间两两比较,其结论完全一致。
例8.2 下表为用动物研究白血病时测得的鼠脾DNA(脱氧核糖核酸)含量,现作方差分析,比较四个不同病情组的均数相差是否显著。
表8.5 鼠脾DNA含量测定值(mg)
| 正常组 | 患自发性 白血病组 | 患移植白血病 | 总 计 | ||
| 甲组 | 乙组 | ||||
| 12.3 | 10.8 | 9.3 | 9.5 | ||
| 13.2 | 11.6 | 10.3 | 10.3 | ||
| 13.7 | 12.3 | 11.1 | 10.5 | ||
| 15.2 | 12.7 | 11.7 | 10.5 | ||
| 15.4 | 13.5 | 11.7 | 10.5 | ||
| 15.8 | 13.5 | 12.0 | 10.9 | ||
| 16.9 | 14.8 | 12.3 | 11.0 | ||
| 17.3 | 12.4 | 11.5 | |||
| 13.6 | |||||
| ∑Xij j | 119.8 | 89.2 | 104.4 | 84.7 | 398.1 |
| ni | 8 | 7 | 9 | 8 | 32 |
| Xi | 14.98 | 12.74 | 11.60 | 10.59 | 12.44 |
| ∑X2ij j | 1815.96 | 1147.32 | 1223.58 | 899.15 | 5086.01 |
| SSi | 21.96 | 10.66 | 12.54 | 2.39 | 47.55 |
1.作检验假设H0:μ1=μ2=μ3=μ4,H1:各总体均数不都相等。α=0.01。
2.用表8.5下部数字计算离均差平方和:简法是先求校正数C=(∑X)2/N=398.12/32,再求
SS总:5086.01-(398.1)2/32=133.40
SS组间:(119.8)2/8+(89.2)2/7+(104.4)2/9+(84.7)2/8-(398.1)2/32=85.85
SS组内:133.40-85.85=47.55
3.列出方差分析表
表8.6 方差分析表
| 变异来源 | 自由度 | 离均差平方和 | 均方 | F |
| 总 计 | 31 | 133.40 | ||
| 组 间 | 3 | 85.85 | 28.62 | 16.48 |
| 组 内 | 28 | 47.55 | 1.70 |
4.查F值表,下结论。看附表8(3),根据求F值时组间均方较大,于是用其自由度3及组内均方的自由度28查得F0.01(3,28)=4.57,今F=16.84>F0.01(3,28)=4.57,故在α=0.01水准处相差显著,P<0.01。四组鼠脾的DNA含量不等。(注:F小于1时无须查表)。
5.为详细分析每两组间的相差情况,作两两比较如下。(因各组例数不等又组数较多,故用Q值法比较)。
(1)将四组均数按大小排列:
| 正常组 | 患白发性 白血病组 | 患移植白血病 | ||
| 甲组 | 乙组 | |||
| DNA平均含量(mg) | 14.98 | 12.74 | 11.60 | 10.59 |
| 秩次 | 1 | 2 | 3 | 4 |
| 样本含量,n | 8 | 7 | 9 | 8 |
(2)求平均例数与标准误:由式(8.10)与式(8.11)计算得
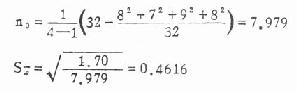
(3)列表比较:
表8.7 均数间两两比较
| A与b (秩次) | 组数a | ∣XA-XB∣ | 界 值 | P值 | |
| q0.05Sχ | q0.01Sχ | ||||
| 4与3 | 2 | 1.01 | 1.36 | 1.86 | >0.05 |
| 4与2 | 3 | 2.15 | 1.65 | 2.14 | <0.01 |
| 4与1 | 4 | 4.39 | 1.83 | 2.32 | <0.01 |
| 3与2 | 2 | 1.14 | 1.36 | 1.86 | >0.05 |
| 3与1 | 3 | 3.38 | 1.65 | 2.14 | <0.01 |
| 2与1 | 2 | 2.24 | 1.36 | 1.86 | <0.01 |
注:本例组内均方的自由度为28但q值表中左侧无28,故用邻近的较小自由度20,此外也可用内插法求出γ为28的q值。
比较结果,除患移植性白血病甲、乙组间;甲组与自发性白血病组间(即按均数大小秩次3与4、3与2间)相差不显著外,余均在α=0.01水准处相差显著,说明正常鼠脾DNA含量最高,患移植白血病乙组的最低。
| 上一页:一、检验的一般步骤 |
| 当前页:二、多个均数间的两两比较 |
| 下一页:第三节 随机单位组设计资料的方差分析 |