四、多组资料的比较
多组资料的比较也是从排秩号开始,但不是直接用秩和进行检验,有的书籍称之为秩检验(rank test),以示与秩和检验有别,其检验假设也较复杂:在处理完全随机设计的资料时,H0:F(X1)=F(X2)=F(X3)=……,即比较的各样本所对应的各总体的分布函数相等,H1:各总体的分布函数不相等或不全相等;在处理随机单位组设计的资料时,H0:P(χij=r)=1/n,即内组各秩号r之概率相等,都是1/n(r=1,2,……,n)而H1为:P=(χij=r)≠1/n。
因不同实验设计所得资料的处理也有别,故下面分别举例说明之。
(一)完全随机设计所得资料的比较
用的方法是单因素多组秩检验,称为Kruskal-Wallis氏法,或H检验。其计算步骤如下。
1.各自排队,统一编秩号。即将各组数据在本组内从小到大排队,见表10.6各含量栏,再将各组数值一起考虑编出统一秩号,见表10.6各“秩号”栏,分属不同组的相同数值用平均秩号;
2.求各组秩号之和R1以及各组数n1:
3.代入下式计算H值:
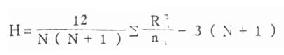
式中N为各组例数之和,Ri和ni为各组的秩号之和以及例数:
4.查表作结论
当比较的组数多于三组,或组数虽只有三组但每组例数大于5时,H值的分布近于自由度等于组数-1的χ2分布,故可用对应的χ2值作界值。当三组比较时每组例数均不超过5时,H值与χ2值有较大偏离,此时可查附表14,直接查得H0.05和H0.01。
例10.6 雄鼠20只随机分为四组,第1、2组在皮肤上涂用放射性锡(Sn113)标记的三乙基硫酸锡,涂后将皮肤暴露于空气中;第3、4组涂药后用密闭小玻璃管套使皮肤与外界空气隔开,三小时后杀死,测肝中放射物,结果如表10.6,试比较各组含量间有无显著相差?
表10.6 白鼠皮肤涂药后,肝中放射性Sn113的含量
| 涂干药后敞开 | 涂湿药后敞开 | 涂干药后密闭 | 涂湿药后密闭 | ||||
| 含量 | 秩号 | 含量 | 秩号 | 含量 | 秩号 | 含量 | 秩号 |
| 0.00 | 1 | 1.82 | 11 | 0.66 | 5 | 3.67 | 14 |
| 0.42 | 2.5 | 2.79 | 12 | 0.71 | 6 | 4.46 | 16 |
| 0.42 | 2.5 | 3.07 | 13 | 0.75 | 7 | 4.51 | 18 |
| 0.59 | 4 | 4.19 | 15 | 0.83 | 8 | 5.07 | 19 |
| 0.97 | 9 | 4.47 | 17 | 1.49 | 10 | 6.02 | 20 |
| Ri | R1=19 | R2=68 | R3=36 | R4=87 | |||
| ni | n1=5 | n2=5 | n3=5 | n4=5 | |||
各组资料各自排队,统一编秩号,以及求各组的秩号之和Ri和例数ni见表10.6
代入式(10.8)得
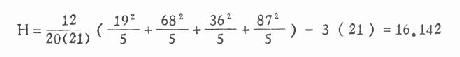
本例组数为4(>3),查χ2值表,ν=4-1=3,得χ20.05,3=7.81,χ20.01,3=11.34,今H>χ20.01,3,故P<0.01,在α=0.01水准上拒绝H0,接受H1,即各组肝中放射性Sn113含量差别显著。
(二)随机单位组设计所得资料的比较
用的方法是双因素多组秩检验,即Friedman氏法。
处理这种资料时可分成两步,对两个因素分别进行检验。现用例10.7说明其计算步骤:
先比较四种防护服对脉搏的影响
1.将穿四种防护服的每一受试者的脉搏数从小到大编秩号,当数值相等时用平均秩号,见表10.7各秩号栏。
2.求各防护服组秩号之和Ri
3.代入式10.9求H值
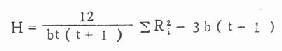
式中t(treatment)为处理组数,b(block)为单位组数。
4.查表作结论
当t>4或t=4且b>5或t=3且b>9时,H值的分布近于自由度ν=t-1时的χ2分布,故可查相应的χ2值与H值比较作出判断:如t、b不能满足上述条件,则所算得的H值与χ2分布有较大偏离,需查附表15作判断。
例10.7 受试者5人,每人穿四种不同的防护服时的脉搏数如表10.7,问四种防护服对脉搏的影响有无显著差别?又五个受试者的脉搏数有无显著差别?
表10.7 比较穿四种防护服时的脉搏数(次/分)
| 受试者 | 防护服A | 防护服B | 防护服C | 防护服D | ||||
| 编 号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 秩号 | 秩号 | 脉搏 | 秩号 |
| 1 | 144.4 | 4 | 143.0 | 3 | 133.4 | 1 | 142.8 | 2 |
| 2 | 116.2 | 2 | 119.2 | 4 | 118.0 | 3 | 110.8 | 1 |
| 3 | 105.8 | 1 | 114.8 | 3 | 113.2 | 2 | 115.8 | 4 |
| 4 | 98.0 | 1 | 120.0 | 3 | 104.0 | 2 | 132.8 | 4 |
| 5 | 103.8 | 2 | 110.6 | 4 | 109.8 | 3 | 100.6 | 1 |
| 秩秩号和Ri | 10 | 17 | 11 | 12 | ||||
t=4b=5
排队、编秩号、求各比较组的Ri见表10.7所示。
将表10.7中各数代入式10.9,得
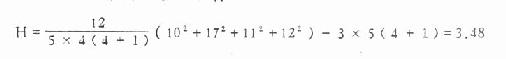
本例t=4,b=5查附表15,得H0.05=7.80,今H>H0.05,故P>0.05,在α=0.05水准上接受H0,无显著差别,故四种防护服对脉搏的影响无显著差别。
再比较五名受试者的脉搏数:
将数据列出(同表10.7),但秩号是按每种防护服中受试者脉搏的数值从小到大编定,然后求出各受试者秩号之和R1,详细见表10.8
表10.8 比较五名受试者的脉搏数
| 受试者 | 防护服A | 防护服B | 防护服C | 防护服D | Ri | ||||
| 编 号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 脉搏 | 秩号 | |
| 1 | 144.4 | 5 | 143.0 | 5 | 133.4 | 5 | 142.8 | 5 | 20 |
| 2 | 116.2 | 4 | 119.2 | 3 | 118.0 | 4 | 110.8 | 2 | 13 |
| 3 | 105.8 | 3 | 114.8 | 2 | 113.2 | 3 | 115.8 | 3 | 11 |
| 4 | 98.0 | 1 | 120.0 | 4 | 104.0 | 1 | 132.8 | 4 | 10 |
| 5 | 103.8 | 2 | 110.6 | 1 | 109.8 | 2 | 100.6 | 1 | 6 |
t=5b=4
将表10.8 所得各数据代入式10.9得
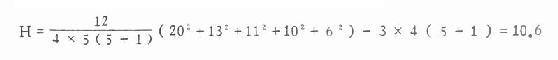
此处t>4,故查ν=5-1=4时的χ2值表,得:χ20.05,4=9.49,χ20.01,4=13.28,今χ20.05,4<H<X20.01,4,故0.05>P>0.01,在α=0.05水准上拒绝H0,接受H1,差别显著;即五名受试者脉搏数相差显著,1号受试者最高,5号受试者最低。
| 上一页:三、两组等级资料的比较 |
| 当前页:四、多组资料的比较 |
| 下一页:五、多组资料间的两两比较 |