| ※中学数学公式定律手册※===>高中代数==>排列、组合、二项式定理 上一页 下一页 | |||
|
分 类 计 数 原 理 | 分 步 计 数 原理 | ||
| 做一件事，完成它有n类不同的办法。第一类办法中有m1种方法，第二类办法中有m2种方法……，第n类办法中有mn种方法，则完成这件事共有：N=m1+m2+…+mn种方法。 | 做一件事，完成它需要分成n个步骤。第一步中有m1种方法，第二步中有m2种方法……，第n步中有mn种方法，则完成这件事共有：N=m1•m2•…•mn种方法。 | ||
|
注意：处理实际问题时，要善于区分是用分类计数原理还是分步计数原理，这两个原理的标志是“分类”还是“分步骤”。 |
|||
| 排 列 | 组 合 | ||
| 从n个不同的元素中取m(m≤n)个元素，按照一定的顺序排成一排，叫做从n个不同的元素中取m个元素的排列。 | 从n个不同的元素中，任取m(m≤n)个元素并成一组，叫做从n个不同的元素中取m个元素的组合。 | ||
|
排 列 数 |
组 合 数 | ||
|
从n个不同的元素中取m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，记为Pnm |
从n个不同的元素中取m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数，记为Cnm | ||
|
选 排 列 数 |
全 排 列 数 |
|
|
|
|
||
|
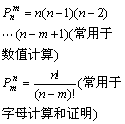
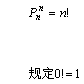
二 项 式 定 理 |
|
||
|
二项展开式的性质 |
(1)项数：n+1项
(2)指数：各项中的a的指数由n起依次减少1，直至0为止；b的指出从0起依次增加1，直至n为止。而每项中a与b的指数之和均等于n 。 (3)二项式系数：
各奇数项的二项式数之和等于各偶数项的二项式的系数之和 |
||
