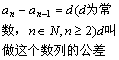
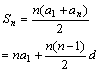
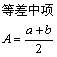

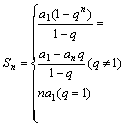
(2)第二步的证明过程中必须使用归纳假设。
| ※中学数学公式定律手册※===>高中代数==>数列 上一页 下一页 | ||||
| 名称 | 定 义 | 通 项 公 式 | 前n项的和公式 | 其它 |
| 数列 | 按照一定次序排成一列的数叫做数列,记为{an} | 如果一个数列{an}的第n项an与n之间的关系可以用一个公式来表示,这个公式就叫这个数列的通项公式 | ||
| 等差数列 |
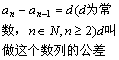
|
|
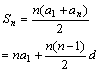
|
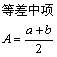
|
| 等比数列 |

|
|
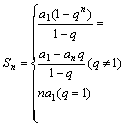
|
|
| 数列前n项和与通项的关系: |
|
|||
| 无穷等比数列所有项的和: |
|
|||
| 数学归纳法 | 适 用 范 围 | 证 明 步 骤 | 注 意 事 项 | |
| 只适用于证明与自然数n有关的数学命题 | 设P(n)是关于自然n的一个命题,如果(1)当n取第一个值n0(例如:n=1或n=2)时,命题成立(2)假设n=k时,命题成立,由此推出n=k+1时成立。那么P(n)对于一切自然数n都成立。 |
(1)第一步是递推的基础,第二步的推理根据,两步缺一不可
(2)第二步的证明过程中必须使用归纳假设。 |
||