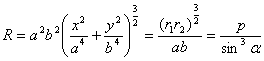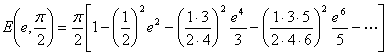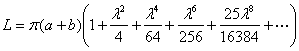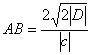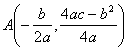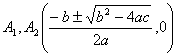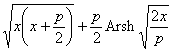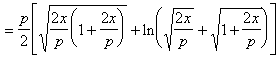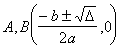§ 5 Quadratic Curve
1. Circle
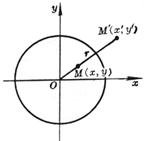
[ Circle equation, center and radius ]
|
Equations and Graphics |
Center and Radius |
|
|
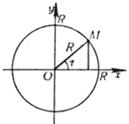
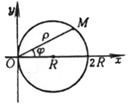
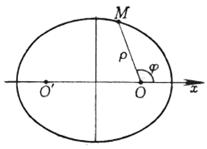
x 2 + y 2 = R 2 or ( parametric equation, t is the angle between the moving diameter OM and the positive direction of the x -axis )
|
|
Center G (0,0) radius r = R
|
|
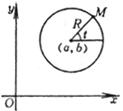
( x - a ) 2 +( y - b ) 2 = R 2 or ( parametric equation, t is the angle between the moving diameter OM and the positive direction of the x -axis ) |
|
Center G ( a , b ) radius r = R
|
|
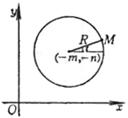
x 2 + y 2 + 2 mx + 2 ny + q = 0 m 2 + n 2 > q r 2 + 2 r ( m cos t + n sin t ) + q = 0 ( polar equation )
|
|
Center G ( - m , - n ) radius
|
|
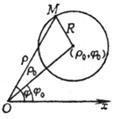
r 2 - 2 rr 0 cos( j - j 0 ) + r 0 2 = R 2 ( polar equation )
|
|
Center G ( r 0 , j 0 ) radius r = R
|
|
x 2 + y 2 = 2 Rx or r = 2 R cos j ( Polar Coordinate Equation ) |
|
Center G ( R , 0) radius r = R
|
|
x 2 + y 2 = 2 Ry or r = 2 R sin j ( Polar Coordinate Equation ) |
|
Center G(0, R ) radius r = R |
[ Circle tangent ]
The equation of the tangent to a point M ( x 0 , y 0 ) on the circle x 2 + y 2 = R 2 is
x 0 x + y 0 y = R 2
The equation of the tangent to a point M ( x 0 , y 0 ) on the circle x 2 + y 2 + 2 mx + 2 ny + q = 0 is
x 0 x + y 0 y + m ( x + x 0 ) + n ( y + y 0 ) + q = 0
[ Intersection of two circles, circle bundle and root axis ]
|
Equations and Graphics |
Formula and Explanation |
|
The intersection of two circles C 1 x 2 + y 2 + 2 m 1 x + 2 n 1 y + q 1 = 0 C 2 x 2 + y 2 + 2 m 2 x + 2 n 2 y + q 2 = 0 The intersection angle of two circles is the angle between their two tangents at the intersection
|
In the formula, q represents the intersection angle of the two circles C1 and C2 , because the coordinates of the intersection point are not included in the formula, so the two intersection angles at the two intersection points must be equal . The two circles C1 and C2 are orthogonal to the condition that 2 m 1 m 2 + 2 n 1 n 2 - q 1 - q 2 = 0
|
|
Circle bundle × root axis of two circles C l C 1 + l C 2 = 0 ( l is a parameter ) or ( l + 1)( x 2 + y 2 ) + 2( m 1 + l m 2 ) x + 2( n 1 + l n 2 ) y + ( q 1 + l q 2 ) = 0 The root axis equation is 2( m 1 - m 2 ) x + 2( n 1 - n 2 ) y + ( q 1 - q 2 ) = 0
|
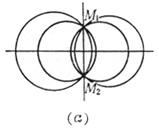
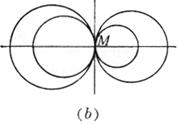
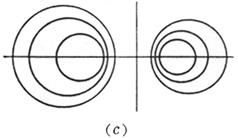
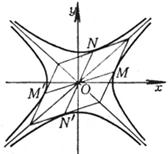
For a certain value of l ( l 1 - 1) , C l represents a circle . When l takes all values ( l 1 - 1) , the whole of the circles represented by C l is called a circle bundle . l = - 1 When , it is a straight line, which is called the root axis of the two circles C1 and C2. The root axis is perpendicular to the connecting center line of C1 and C2 , and the center of any circle C1 in the bundle is at the center of C1 and C2 . connected to the central line, and the ratio of the sub-connected central lines is equal to l . ( a ) If C 1 and C 2 intersect at two points M 1 , M 2 , then all circles in the bundle pass through the two intersection points M 1 , M 2 , and their root axis is their common chord. At this time circular bundle is called Coaxial circle system ( Fig. ( a )). ( b ) If C1 and C2 are tangent to a point M , then all circles in the bundle are tangent , and the root axis is the common tangent at the point M ( Figure ( b ) ) . ( c ) If C1 and C2 do not intersect, all circles in the bundle do not intersect, and the root axis does not intersect with all circles in the bundle ( Figure ( c ) ) . Draw tangents to two circles C1 and C2 from point P , and the locus of point P with equal tangent lengths is the root axis . The root axis of the two concentric circles is a straight line from the common center to infinity . Among the three circles The root axes of each pair of circles ( three in total ) intersect at a point, which is called the root center . If the three circle centers are collinear, the root center is at infinity .
|
[ Inversion ] Let C be a certain circle, O be the center of the circle, r be the radius ( Fig. 7.1) , for any point M on the plane , there is a point M ¢ corresponding to it . Make the following two conditions are satisfied:
( i ) O , M , M ¢ are collinear,
( ii ) OM × OM ¢ = r 2 ,
This kind of point M ¢ is called the inversion point of point M about the fixed circle C , C is called the inversion circle, O is the inversion center, and r is the inversion radius .
Since the relationship between M and M ¢ is symmetric, M is also the inversion point of M ¢ . Since r 2 > 0 , both M and M ¢ are on the same side of O. The correspondence between M and M ¢ is called about Inversion of definite circle C.
Taking O as the origin, the corresponding equations of all inversion points M ( x , y ) and M ¢ ( x ¢ , y ¢ ) are
![]()
Inversion has the properties:
|
Figure 7.1 |
1 ° A straight line not passing through the inversion center becomes a circle passing through the inversion center .
2 ° A circle passing through the inversion center becomes a straight line that does not pass through the inversion center .
3 ° becomes itself by a straight line through the center of the inversion .
4 ° A circle that does not pass through the inversion center becomes a circle that does not pass through the inversion center .
The 5 ° inversion circle becomes itself .
6 ° The circle orthogonal to the inversion circle becomes itself, and its inverse is true .
7 ° If the two curves C 1 , C 2 intersect at a point M , the inversion curves C 1 ¢ , C 2 ¢ must intersect at the inversion point M ¢ of M.
8 ° If the two curves C 1 , C 2 are tangent at a point M , then the inverted curves C 1 ¢ , C 2 ¢ must be tangent at the inversion point M ¢ of M.
The intersection angle of the two curves of 9 ° is unchanged under the inversion . It can be seen that the inversion is a conformal transformation .
2. Ellipse
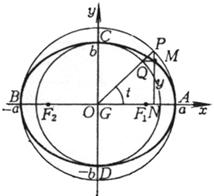
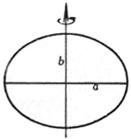
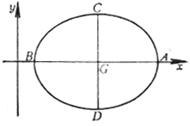
1. Basic Elements of Ellipse
Main axis ( symmetry axis )
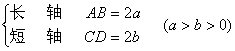
Vertices A , B , C , D
Ellipse center G
Focus F 1 , F 2
focal length
![]()
Eccentricity _ ![]()
compression factor ![]()
焦点参数 ![]() (等于过焦点且垂直于长轴的弦长之半,即F1H)
(等于过焦点且垂直于长轴的弦长之半,即F1H)
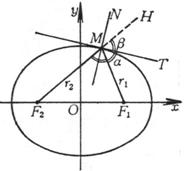
焦点半径 r1, r2(椭圆上一点(x, y)到焦点的距离)
r1 = a - ex, r2 = a + ex
直 径 PQ(通过椭圆中心的弦)
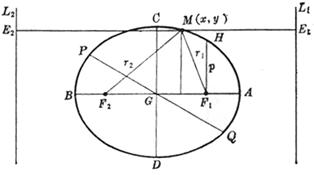
图 7.2
共轭直径 二直径斜率为![]() ,且满足
,且满足![]()
准
线 L1和L2(平行于短轴,到短轴的距离为![]() )
)
2.椭圆的方程、顶点、中心与焦点
|
方 程 与 图 形 |
vertex · center · focus |
|
|
( parametric equation, t is the angle between the radius of the concentric circle ( radius a , b ) corresponding to point M and the positive direction of the x -axis )
|
|
Vertices A , B ( ± a , 0) C , D (0, ± b ) Center G (0,0) Focus F 1 , F 2 ( ± c ,0)
|
|
( t same as above ) |
|
Vertices A , B ( g ± a , h ) C , D ( g , h ± b ) Center G ( g , h ) Focus F 1 , F 2 ( g ± c , h )
|
|
|
|
Vertices A , B (0, ± a ) C , D ( ± b , 0) Center G (0, 0) Focus F 1 , F 2 (0, ± c )
|
|
( Polar coordinate equation, the pole is located at the focus of the ellipse, the polar axis is the ray from the focus to the nearest vertex, j is the polar angle, p , e are as described above ) |
|
long axis short axis focal length
|
3. properties of an ellipse
A 1 ° ellipse is the locus ( r 1 + r 2 = 2 a ) of a moving point M whose distances to two fixed points ( i.e. the focal points ) have a constant sum ( i.e. the major axis ) .
A 2 ° ellipse is also the locus of a moving point M whose ratio of the distance to a certain point ( ie, one of the focal points ) to a certain straight line ( ie, a directrix L ) is a constant ( ie, eccentricity ) less than 1 ( MF 1 / ME 1 = MF 2 / ME 2 = e ).
A 3 ° ellipse is obtained by compressing a circle with radius a along the y -axis in proportion ( ie, the compressibility factor ) . ![]()
The equation of the tangent ( MT ) at a point M ( x 0 , y 0 ) on a 4 ° ellipse is
![]()
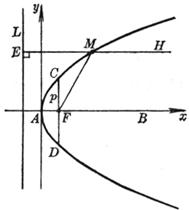
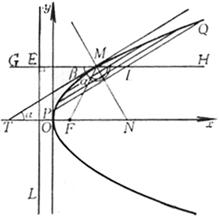
The tangent line bisects the outer angle (i.e. ∠ F 1 MH ) between the two focal radii of point M ( i.e. a = b , ) , and the normal MN of point M bisects the inner angle ( i.e. ∠ F 1 MF 2 ) ( Figure 7.3 ) .![]()
If the slope of the tangent ( MT ) of the ellipse is k , then its equation is
![]()
|
Figure 7.3 |
The positive and negative signs in the formula represent the two tangents at the two ends of the diameter .
|
Figure 7.4 |
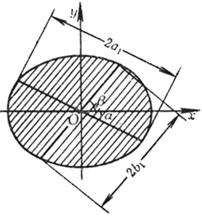
Any diameter of a 5 ° ellipse bisects the chord parallel to its conjugate diameter ( Figure 7.4)
If the lengths of the two conjugate diameters are 2 a 1 and 2 b 1 respectively , and the included angles ( acute angles ) between the two diameters and the long axis are a and b respectively , then a 1 b 1 sin( a + b ) = ab
a 1 2 + b 1 2 = a 2 + b 2
The product of the focal radii of any point M on a 6 ° ellipse is equal to the square of its corresponding semi-conjugate diameter .
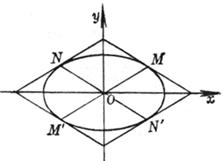
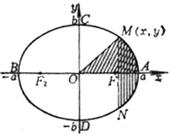
7 ° Let MM ¢ , NN ¢ be the two conjugate diameters of the ellipse , through M , M ¢ make a straight line parallel to NN ¢ ; The area of the quadrilateral is a constant 4 ab ( Figure 7.5).
|
Figure 7.5 |
4. Calculation formula of each quantity of ellipse
![]()
|
Ellipse quantities |
Calculation formula |
||
|
[ radius of curvature ] R |
where r 1 , r 2 are the focus radius , p is the focus parameter , a is the angle between the focus radius of the point M ( x , y ) and the tangent . In particular , the curvature radius of the vertex |
||
|
[ arc length ] |
where e is the eccentricity |
||
|
[ perimeter ] L
|
In the formula , set , then |
||
|
[ area ] S |
sector ( OAM ) area arcuate ( MAN ) area Ellipse area S = p ab |
||
|
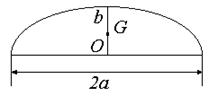
[ geometric center of gravity ] G
|
Oval G and O coincide _ half oval ( a , b are the semi-axis lengths of the ellipse ) |
|
|
|
[ Moment of inertia ] J
|
The axis of rotation of the ellipse passes through the b axis where m is the mass |
|
|
3. Hyperbola
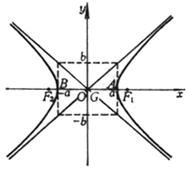
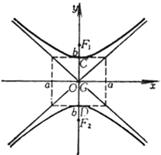
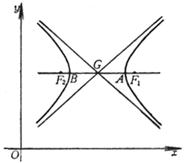
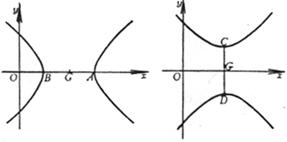
1.[1051] Basic Elements of Hyperbola
Main axis ( symmetry axis )
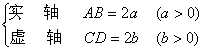
|
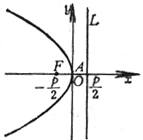
Figure 7.6 |
Vertices A , B
Center G
Focus F 1 , F 2
Focal length F 1 F 2
= 2 c , ![]()
Eccentricity _ ![]()
Focus parameter ( equal to the sum of the chord lengths that are over-focus and perpendicular to the real axis ![]()
half , i.e. F 1 H )
Focus radius r 1 , r 2 ( the distance from a point ( x , y ) on the hyperbola to the focus ,
i.e. MF 1 , MF 2 )
r 1 = ± ( ex - a ), r 2 = ± ( ex + a )
Diameter PQ ( chord through center )
Conjugate diameter two diameter slopes are k , k ¢ , and satisfy ![]()
Directives L 1 and L 2 ( perpendicular to the real axis , the distance from the center ) ![]()
2 . Equation, vertex, center, focus, and asymptotes of a hyperbola
|
Equations and Graphics |
vertex, center, focus, asymptote |
||
|
or
( parametric equation ) or |
|
Vertices A , B ( ± a ,0) Center G (0,0) Focus F 1 , F 2 ( ± c ,0) asymptote _
|
|
|
( and form a conjugate hyperbola )
|
|
vertex center focus
asymptote _ |
|
|
|
|
vertex
center focus
asymptote _
|
|
|
equation |
with graphics |
vertex, center, focus, asymptote |
|
|
( Polar coordinate equation . The pole is located at a focal point, and the polar axis is the ray from the focal point back to the vertex, p , e are as described above . From this equation, only one can be determined, and the other can be obtained by symmetry )
|
|
real axis imaginary axis
focal length
|
|
|
|
vertex center focus
( same sign when k > 0 , different sign when k < 0 ) shaft length
asymptote _ |
||
|
( equiaxed hyperbola )
|
|
Vertices
( same sign when D < 0 , different sign when D > 0 )
center
shaft length asymptote _
|
|
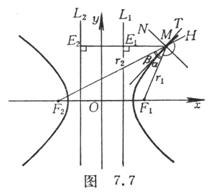 3. Properties of Hyperbola
3. Properties of Hyperbola
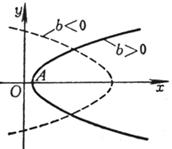
A 1 ° hyperbola is the locus of a moving point M whose distance to two fixed points ( focal points ) is a constant difference ( equal to the real axis 2 a ) ( so that each point belongs to one branch of the hyperbola, and each point belongs to the other. one ). ![]()
![]()
A 2 ° hyperbola is also the locus ( ) of the moving point M where the ratio of the distance to a certain point ( one of the focal points ) to the distance to a certain straight line ( directive line L 1 ) is a constant ( ie eccentricity ) greater than 1 . ![]()
The equation of the tangent ( MT ) at a point M on a 3 ° hyperbola is ![]()
![]()
|
Figure 7.8 |
It bisects the interior angle ( ie ) between the radii of the two focal points at point M , while the normal MN at point M bisects the outer angle ( ie ) ( Figure 7.7) .![]()
![]()
![]()
If the slope of the tangent of a hyperbola is k , then the equation of its tangent is
![]()
The positive and negative signs in the formula represent the two tangents at the two ends of the diameter .
4 ° The tangent line segment TT1 between the two asymptotes is bisected by the tangent point M ( TM = MT1 ) , and ![]()
D OTT 1 area ,![]()
Area of parallelogram OJMI ( shaded area in Figure 7.8 )
![]()
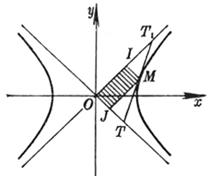
Any diameter of a 5 ° hyperbola bisects the chord parallel to the conjugate diameter ( Figure 7.9)
|
Figure 7.9 |
If the lengths of the two conjugate diameters are 2 a 1 , 2 b 1 respectively , and the included angles ( acute angles ) between the two diameters and the real axis are a and b respectively ( a < b ) , then
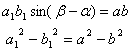
The product of the focal radii of any point M on the 6 ° hyperbola is equal to the square of its corresponding semi-conjugate diameter .
|
Figure 7.10 |
7 ° Let MM ¢ , NN ¢ be the two conjugate diameters of the hyperbola , and draw straight lines parallel to NN ¢ through M , M ¢ respectively ; The area of a parallelogram is a constant 4 ab ( Figure 7.10).
4. The formula for calculating the quantities of the hyperbola
|
|
![]()
|
hyperbolic quantities |
Calculation formula |
|
[ radius of curvature ] R
|
where r 1 , r 2 are the focal radius, p is the focal parameter, a is the angle between the focal radius of the point M ( x , y ) and the tangent, in particular, the curvature radius of the vertices A , B
|
|
hyperbolic quantities |
Calculation formula |
|
[ arc length ]
|
where e is the eccentricity |
|
[ area ] S
|
The area of the bow ( AMN ) : Area of OAMI : Here OI , OJ are asymptotes, MI // OJ |
4. Parabola
|
Figure 7.11 |
1. basic elements of a parabola
Axis AB of the parabola
vertex A
Focus F
The focus parameter p ( equal to overfocus and perpendicular to the axis
half the length of the string CD )
Focus radius MF ( a point on the parabola to the focus
distance )
Diameter EMH ( direction parallel to the axis of the parabola)
line )
Directrix L ( perpendicular to the axis of the parabola, the distance from the vertex A equals , and the distance from the focus F equals p )
![]()
2. Equations, vertices, focus and directrix of a parabola
|
Equations and Graphics |
Vertex · Focus · Directive |
|
|
( Polar coordinate equation, the pole is located at the focus F , the polar axis coincides with the axis of the parabola, and faces away from the vertex ) |
|
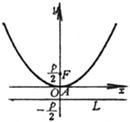
Vertex A (0, 0) focus
alignment _ |
|
|
|
Vertex A (0, 0) focus
alignment _
|
|
Equations and Graphics |
Vertex · Focus · Directive |
|
|
|
|
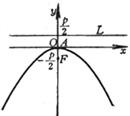
Vertex A (0, 0) focus
alignment _ |
|
|
|
Vertex A (0, 0) focus
alignment _ |
|
|
|
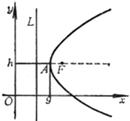
Vertex A ( g , h ) focus
alignment _
|
|
|
|
Vertex A ( g , h ) focus
alignment _ |
|
|
|
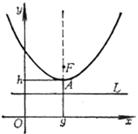
vertex
( When a > 0 , the opening is up, When a < 0 , the opening is down ) focus parameter Intersection with the x -axis
vertex
focus parameter
|
3. properties of a parabola
|
Figure 7.12 |
A 1 ° parabola is the locus of a moving point M ( MF ¢ = ME ) whose distance to a certain point F ( the focal point ) is equal to the distance to a certain straight line L ( the directrix ) ( Figure 7.12)
The equation of the tangent MT at a point on a 2 ° parabola is ![]()
![]()
It bisects the angle ( D FMG ) between the focal radius of point M and the diameter ( D FMT = D TMG ) , and all chords parallel to the tangent MT are bisected by the diameter of point M ( PI = IQ ).
If the slope of the tangent to a parabola is k , then the equation of its tangent is
![]()
The angle between any two tangents of a 3 ° parabola is equal to half the angle between the focal radii of the two tangent points .
4 ° From the focus F , draw the perpendicular to the tangent of the parabola at point M , then the trajectory of the foot is the tangent at the vertex .
4. The formula for calculating the quantities of the parabola
![]()
|
Parabolic quantities |
Calculation formula |
|
[ radius of curvature ] R
|
where a is the angle between the tangent of the point M ( x , y ) and the main axis, and n is the length of the normal MN . In particular, the radius of curvature of the vertex R 0 = p |
|
[ arc length ]
|
|
|
[ area ] S |
The area of the arc ( MOD ) = the area of the parallelogram ( MBCD ) which is
Here MD is the bow chord length , CD is parallel to the major axis , BC is tangent to the parabola , h is the height of the parallelogram ( that is, the arch height ), in particular , |
|
[ geometric center of gravity ] G |
The center of gravity of the bow ( MOD ) ( BC is parallel to MD , P is the tangent point , PQ is parallel to Ox ) |
5. General quadratic curve
1 . General Properties of Quadratic Curves
The ellipse, hyperbola, parabola, etc. listed above , their equations are quadratic about x , y , and the general quadratic equation about x, y is in the form of
![]()
The curve it represents is called a general quadratic curve . Here are some common properties of them .
[ Intersection point of a straight line and a quadratic curve ] A straight line and a quadratic curve intersect at two points ( real , imaginary , coincident ).
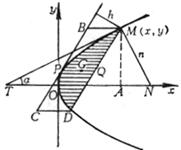
[ Diameter and center of quadratic curve ] The midpoint of the chord of a quadratic curve parallel to the known direction is on a straight line , and it is called the diameter of the quadratic curve , which bisects a certain set of chords . The number of directions is a , b , the equation of the diameter is
![]()
or rewritten as
![]()
It can be seen that the diameters of the quadratic curve form a bundle of straight lines . Any diameter in the bundle passes through the intersection of the following two straight lines :
![]()
1 ° ie . ![]()
![]()
At this time, all the diameters of the quadratic curve pass through the same point , which is called the center . This kind of curve is called a centered quadratic curve . The coordinates of the center are
![]()
2 ° ie ![]()
![]()
(i)
At this time, the curve has no center ;![]()
(ii) At this time, the curve has an infinite number of centers , that is, the centers are on the same line ( center line ).![]()
These two curves are called centerless quadratic curves .
[ Main axis ( or axis of symmetry ) of quadratic curve] If the diameter is perpendicular to the chord bisected by it , it is called the main axis ( axis of symmetry ) of the quadratic curve. The concentric quadratic curve has a real main axis ; the centered quadratic curve A curve has two real major axes , they are perpendicular to each other , and the intersection is the center .
[ Tangent and normal of quadratic curve ]
The equation of the tangent to a point on a quadratic curve is![]()
![]()
The line perpendicular to the tangent of the quadratic curve at point M is called the normal at point M , and its equation is
![]()
2 . Invariants of Quadratic Curves
From the equation of the general quadratic curve
![]() (1)
(1)
The following three functions are composed of the coefficients of :
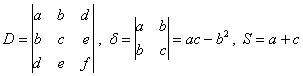
It is called the invariant of the quadratic curve , that is, after the coordinate transformation , these quantities are unchanged . The determinant D is called the discriminant of the quadratic equation (1) .
3 . Standard Equations and Shapes of Quadratic Curves
|
invariant _ |
Standard equation after coordinate transformation |
Curve shape |
||
|
have Heart two Second-rate song String |
|
|
in the formula A , C are characteristic equations |
|
|
|
A pair of imaginary lines with a common real point |
|||
|
|
|
hyperbola |
||
|
|
intersect two lines |
|||
|
|
|
|
||
|
without Heart two Second-rate song String |
|
in the formula |
parabola |
|
|
|
|
|
||
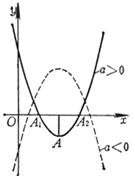
4 . Several cases of quadratic curve![]()
|
A |
graphics |
Vertex·Center·Focus Parameters |
|
parabola |
|
vertex focus parameter |
|
oval |
|
vertex in center |
|
hyperbola |
|
5. Conical section
Quadratic curves are all stubs that cut a regular conic surface with a plane . Therefore, quadratic curves are also called conic stubs (Figure 7.13 )
 |
When cutting a regular cone with a plane P , if P does not pass through the top of the cone and is not parallel to any generatrix , the sectional line is an ellipse ; if P does not pass through the apex of the cone but is parallel to a generatrix , the sectional line is a parabola ; if When P does not pass through the top of the cone and is parallel to the two generatrixes , the sectional line is a hyperbola ; if P is perpendicular to the cone axis , the sectional line is a circle .
If P passes through the top of the cone , the ellipse becomes a point , the hyperbola becomes a pair of intersecting straight lines , and the parabola becomes a straight line tangent to P and the cone .