|
|
|

A puzzle introduced by Sam Loyd in 1878. It consists of 15 squares numbered from 1 to 15 which are placed in a ![]() box leaving one position out of the 16 empty. The goal is to rearrange the squares from a given arbitrary starting
arrangement by sliding them one at a time into the configuration shown above. For some initial arrangements, this
rearrangement is possible, but for others, it is not.
box leaving one position out of the 16 empty. The goal is to rearrange the squares from a given arbitrary starting
arrangement by sliding them one at a time into the configuration shown above. For some initial arrangements, this
rearrangement is possible, but for others, it is not.
To address the solubility of a given initial arrangement, proceed as follows. If the Square containing the number
![]() appears ``before'' (reading the squares in the box from left to right and top to bottom)
appears ``before'' (reading the squares in the box from left to right and top to bottom) ![]() numbers which are less
than
numbers which are less
than ![]() , then call it an inversion of order
, then call it an inversion of order ![]() , and denote it
, and denote it ![]() . Then define
. Then define
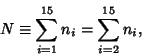

![]() (2 precedes 1) and all other
(2 precedes 1) and all other ![]() , so
, so ![]() and the puzzle cannot be solved.
and the puzzle cannot be solved.
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York:
Dover, pp. 312-316, 1987.
Bogomolny, A. ``Sam Loyd's Fifteen.''
http://www.cut-the-knot.com/pythagoras/fifteen.html.
Bogomolny, A. ``Sam Loyd's Fifteen [History].''
http://www.cut-the-knot.com/pythagoras/history15.html.
Johnson, W. W. ``Notes on the `15 Puzzle. I.''' Amer. J. Math. 2, 397-399, 1879.
Kasner, E. and Newman, J. R. Mathematics and the Imagination. Redmond, WA: Tempus Books, pp. 177-180, 1989.
Kraitchik, M. ``The 15 Puzzle.'' §12.2.1 in Mathematical Recreations. New York: W. W. Norton, pp. 302-308, 1942.
Story, W. E. ``Notes on the `15 Puzzle. II.''' Amer. J. Math. 2, 399-404, 1879.
|
|
|
© 1996-9 Eric W. Weisstein