|
|
|
A formal extension of the Hypergeometric Function to two variables, resulting in four kinds of functions (Appell 1925),
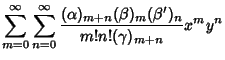 |
|||
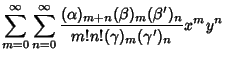 |
|||
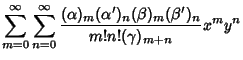 |
|||
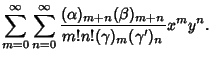 |
Appell defined the functions in 1880, and Picard showed in 1881 that they may all be expressed by
Integrals of the form
References
Appell, P. ``Sur les fonctions hypergéométriques de plusieurs variables.'' In Mémoir. Sci. Math.
Paris: Gauthier-Villars, 1925.
Bailey, W. N. Generalised Hypergeometric Series.
Cambridge, England: Cambridge University Press, p. 73, 1935.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press,
p. 1461, 1980.