An integral is a mathematical object which can be interpreted as an Area or a generalization of Area.
Integrals, together with Derivatives, are the fundamental objects of Calculus.
Other words for integral include Antiderivative and Primitive. The
Riemann Integral is the simplest integral definition and the only one usually encountered in elementary
Calculus. The Riemann Integral of the function 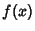 over
over 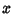 from
from 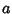 to
to 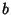 is written
is written
 |
(1) |
Every definition of an integral is based on a particular Measure. For instance, the Riemann Integral is
based on Jordan Measure, and the Lebesgue Integral is based on Lebesgue Measure. The process of
computing an integral is called Integration (a more archaic term for Integration is Quadrature), and
the approximate computation of an integral is termed Numerical Integration.
There are two classes of (Riemann) integrals: Definite Integrals
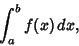 |
(2) |
which have upper and lower limits, and Indefinite Integrals, which are written without
limits. The first Fundamental Theorem of Calculus allows
Definite Integrals to be computed in terms of Indefinite Integrals,
since if 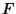 is the Indefinite Integral for
is the Indefinite Integral for 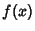 , then
, then
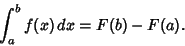 |
(3) |
Wolfram Research
maintains a web site which
will integrate many common (and not so common) functions. However, it cannot solve some simple integrals such as
![\begin{displaymath}
\int \left[{{d\over dx}(x\sqrt{\sin x}\,)}\right]\,dx = \int\left({{x\cos x\over 2\sqrt{\sin x}}+\sqrt{\sin{x}}}\right)\,dx
\end{displaymath}](i_620.gif) |
(4) |
![\begin{displaymath}
\int \left[{{d\over dx} L_2(x\ln x)}\right]\,dx =-\int\left[{(\ln x+1)\ln(1-x\ln x)\over x\ln x}\right]\,dx,
\end{displaymath}](i_621.gif) |
(5) |
where 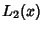 is the Dilogarithm. Mathematica
is the Dilogarithm. Mathematica
 3.0 (Wolfram Research, Champaign, IL) gives an incorrect answer of
3.0 (Wolfram Research, Champaign, IL) gives an incorrect answer of
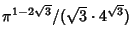 to
to
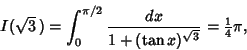 |
(6) |
although integrals of this type remain unevaluated in Mathematica 4.0. Integrals of this form
 |
(7) |
have a ``trick'' solution which takes advantage of the trigonometric identity
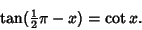 |
(8) |
Letting
 ,
,
Here is a list of common Indefinite Integrals:
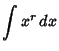 |
 |
 |
(10) |
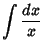 |
 |
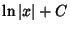 |
(11) |
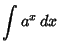 |
 |
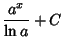 |
(12) |
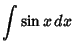 |
 |
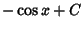 |
(13) |
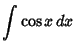 |
 |
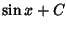 |
(14) |
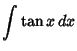 |
 |
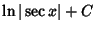 |
(15) |
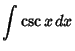 |
 |
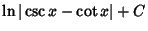 |
(16) |
| |
 |
![$\displaystyle \ln\left[{\tan({\textstyle{1\over 2}}x)}\right]+C$](i_648.gif) |
(17) |
| |
 |
 |
(18) |
 |
 |
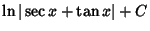 |
(19) |
| |
 |
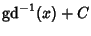 |
(20) |
 |
 |
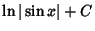 |
(21) |
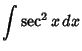 |
 |
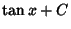 |
(22) |
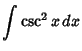 |
 |
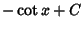 |
(23) |
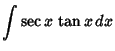 |
 |
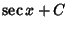 |
(24) |
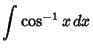 |
 |
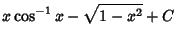 |
(25) |
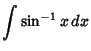 |
 |
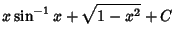 |
(26) |
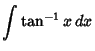 |
 |
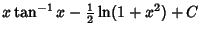 |
|
| |
|
|
(27) |
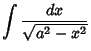 |
 |
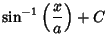 |
(28) |
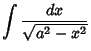 |
 |
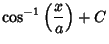 |
(29) |
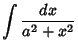 |
 |
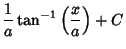 |
(30) |
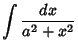 |
 |
 |
(31) |
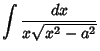 |
 |
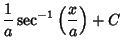 |
(32) |
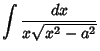 |
 |
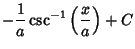 |
(33) |
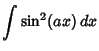 |
 |
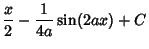 |
(34) |
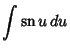 |
 |
 |
(35) |
 |
 |
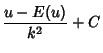 |
(36) |
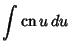 |
 |
 |
(37) |
 |
 |
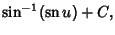 |
(38) |
where 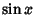 is the Sine;
is the Sine; 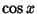 is the Cosine;
is the Cosine; 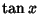 is the Tangent;
is the Tangent;  is the
Cosecant;
is the
Cosecant; 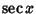 is the Secant;
is the Secant; 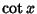 is the Cotangent;
is the Cotangent; 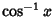 is the Inverse
Cosine;
is the Inverse
Cosine; 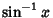 is the Inverse Sine;
is the Inverse Sine; 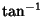 is the Inverse Tangent;
is the Inverse Tangent;
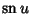 ,
,
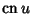 , and
, and
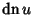 are Jacobi Elliptic Functions;
are Jacobi Elliptic Functions; 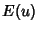 is a complete Elliptic Integral of the Second Kind; and
is a complete Elliptic Integral of the Second Kind; and
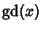 is
the Gudermannian Function.
is
the Gudermannian Function.
To derive (15), let
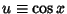 , so
, so
 and
and
To derive (16), let
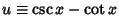 , so
, so
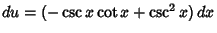 and
and
To derive (19), let
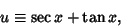 |
(41) |
so
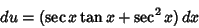 |
(42) |
and
To derive (21), let
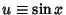 , so
, so 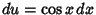 and
and
Differentiating integrals leads to some useful and powerful identities, for instance
 |
(45) |
which is the first Fundamental Theorem of Calculus. Other derivative-integral
identities include
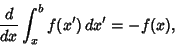 |
(46) |
the Leibniz Integral Rule
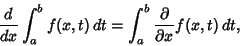 |
(47) |
and its generalization
 |
(48) |
If 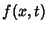 is singular or Infinite, then
is singular or Infinite, then
![\begin{displaymath}
{d\over dx} \int_a^x f(x,t)\,dx = {1\over x-a} \int_a^x \lef...
... \partial x} + (t-a){\partial f\over\partial t}+f}\right]\,dt.
\end{displaymath}](i_726.gif) |
(49) |
Other integral identities include
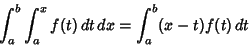 |
(50) |
 |
(51) |
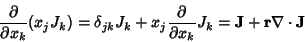 |
(52) |
Integrals of the form
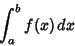 |
(54) |
with one Infinite Limit and the other Nonzero may be expressed as finite integrals over transformed functions. If 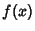 decreases at least as fast as
decreases at least as fast as 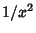 , then let
, then let
and
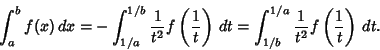 |
(58) |
If 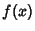 diverges as
diverges as 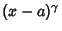 for
for
![$\gamma\in [0, 1]$](i_743.gif) , let
, let
and
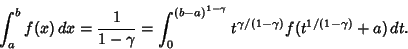 |
(62) |
If 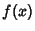 diverges as
diverges as 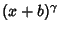 for
for
![$\gamma\in [0, 1]$](i_743.gif) , let
, let
and
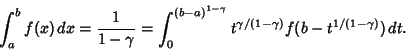 |
(66) |
If the integral diverges exponentially, then let
and
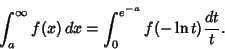 |
(70) |
Integrals with rational exponents can often be solved by making the substitution 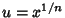 , where
, where 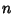 is the
Least Common Multiple of the Denominator of the exponents.
is the
Least Common Multiple of the Denominator of the exponents.
Integration rules include
 |
(71) |
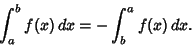 |
(72) |
For 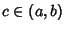 ,
,
 |
(73) |
If 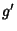 is continuous on
is continuous on ![$[a,b]$](i_765.gif) and
and 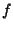 is continuous and has an antiderivative on an Interval containing the values of
is continuous and has an antiderivative on an Interval containing the values of
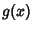 for
for
 , then
, then
 |
(74) |
Liouville  showed that the integrals
showed that the integrals
 |
(75) |
cannot be expressed as terms of a finite number of elementary functions. Other irreducibles include
 |
(76) |
Chebyshev proved that if 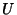 ,
, 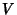 , and
, and 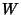 are Rational Numbers, then
are Rational Numbers, then
 |
(77) |
is integrable in terms of elementary functions Iff 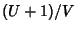 ,
, 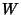 , or
, or 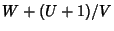 is an Integer (Ritt 1948, Shanks 1993).
is an Integer (Ritt 1948, Shanks 1993).
There are a wide range of methods available for Numerical Integration. A good source for such techniques is Press et al.
(1992). The most straightforward numerical integration technique uses the Newton-Cotes Formulas (also called
Quadrature Formulas), which approximate a function tabulated at a sequence of regularly spaced
Intervals by various degree Polynomials. If the endpoints are tabulated, then the 2-
and 3-point formulas are called the Trapezoidal Rule and Simpson's Rule, respectively. The 5-point formula is
called Bode's Rule. A generalization of the Trapezoidal Rule is Romberg Integration, which can yield
accurate results for many fewer function evaluations.
If the analytic form of a function is known (instead of its values merely being tabulated at a fixed number of points), the best
numerical method of integration is called Gaussian Quadrature. By picking the optimal Abscissas at
which to compute the function, Gaussian quadrature produces the most accurate approximations possible. However, given the speed
of modern computers, the additional complication of the Gaussian Quadrature formalism often makes it less desirable than
the brute-force method of simply repeatedly calculating twice as many points on a regular grid until convergence is obtained. An
excellent reference for Gaussian Quadrature is Hildebrand (1956).
See also A-Integrable, Abelian Integral, Calculus, Chebyshev-Gauss Quadrature, Chebyshev
Quadrature, Darboux Integral, Definite Integral, Denjoy Integral, Derivative, Double
Exponential Integration, Euler Integral, Fundamental Theorem of Gaussian Quadrature, Gauss-Jacobi
Mechanical Quadrature, Gaussian Quadrature, Haar Integral, Hermite-Gauss Quadrature, Hermite
Quadrature, HK Integral, Indefinite Integral, Integration, Jacobi-Gauss Quadrature,
Jacobi Quadrature, Laguerre-Gauss Quadrature, Laguerre Quadrature, Lebesgue Integral,
Lebesgue-Stieltjes Integral, Legendre-Gauss Quadrature, Legendre Quadrature, Lobatto
Quadrature, Mechanical Quadrature, Mehler Quadrature, Newton-Cotes Formulas, Numerical
Integration, Peron Integral, Quadrature, Radau Quadrature, Recursive Monotone Stable
Quadrature, Riemann-Stieltjes Integral, Romberg Integration, Riemann Integral, Stieltjes
Integral
References
Beyer, W. H. ``Integrals.'' CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 233-296, 1987.
Bronstein, M. Symbolic Integration I: Transcendental Functions. New York: Springer-Verlag, 1996.
Gordon, R. A. The Integrals of Lebesgue, Denjoy, Perron, and Henstock. Providence, RI: Amer. Math. Soc., 1994.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, 1993.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 319-323, 1956.
Piessens, R.; de Doncker, E.; Uberhuber, C. W.; and Kahaner, D. K. QUADPACK: A Subroutine Package for Automatic Integration.
New York: Springer-Verlag, 1983.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Integration of Functions.'' Ch. 4 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 123-158, 1992.
Ritt, J. F. Integration in Finite Terms. New York: Columbia University Press, p. 37, 1948.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 145, 1993.
Wolfram Research. ``The Integrator.'' http://www.integrals.com
© 1996-9 Eric W. Weisstein
1999-05-26
![]() over
over ![]() from
from ![]() to
to ![]() is written
is written
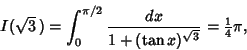
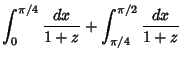
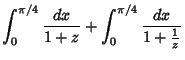
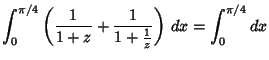
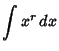

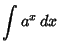
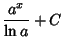
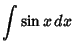
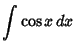
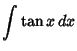
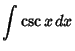



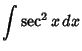
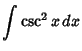
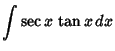
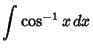
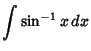
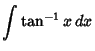
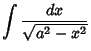
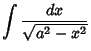
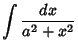
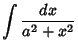
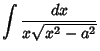
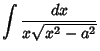
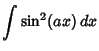
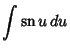

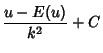
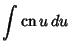

![]() , so
, so
![]() and
and
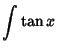
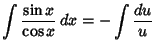
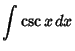

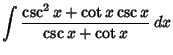
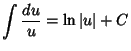

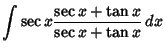
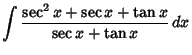
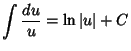

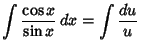


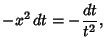
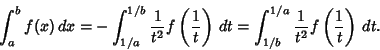
![]() , where
, where ![]() is the
Least Common Multiple of the Denominator of the exponents.
is the
Least Common Multiple of the Denominator of the exponents.

![]() showed that the integrals
showed that the integrals