|
|
|
Seeks to obtain the best numerical estimate of an integral by picking optimal Abscissas ![]() at which
to evaluate the function
at which
to evaluate the function ![]() . The Fundamental Theorem of Gaussian Quadrature states that the optimal
Abscissas of the
. The Fundamental Theorem of Gaussian Quadrature states that the optimal
Abscissas of the ![]() -point Gaussian Quadrature Formulas are precisely the
roots of the orthogonal Polynomial for the same interval and Weighting Function. Gaussian quadrature is optimal
because it fits all Polynomials up to degree
-point Gaussian Quadrature Formulas are precisely the
roots of the orthogonal Polynomial for the same interval and Weighting Function. Gaussian quadrature is optimal
because it fits all Polynomials up to degree ![]() exactly. Slightly less optimal fits are obtained
from Radau Quadrature and Laguerre Quadrature.
exactly. Slightly less optimal fits are obtained
from Radau Quadrature and Laguerre Quadrature.
| Interval | ||
| 1 | ||
|
|
||
|
|
||
|
|
||
|
|
To determine the weights corresponding to the Gaussian Abscissas, compute a Lagrange Interpolating
Polynomial for ![]() by letting
by letting
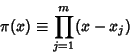 |
(1) |
![\begin{displaymath}
\pi'(x_j)=\left[{d\pi\over dx}\right]_{x=x_j} = \prod_{\scriptstyle i=1\atop\scriptstyle i\not= j}^m (x_j-x_i).
\end{displaymath}](g_1042.gif) |
(2) |
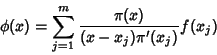 |
(3) |
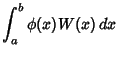 |
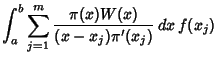 |
||
 |
(4) |
| (5) |
| (6) |
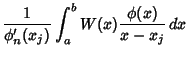 |
|||
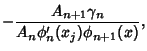 |
(7) |
| (8) |
| (9) |
| (10) |
| (11) |
Other curious identities are
![\begin{displaymath}
\sum_{k=0}^m {[\phi_k(x)]^2\over\gamma_k} = {A_m\over A_{m+1}\gamma_m} [\phi_{m+1}'(x)\phi_m(x)-\phi_m'(x)\phi_{m+1}(x)]
\end{displaymath}](g_1064.gif) |
(12) |
![\begin{displaymath}
\sum_{k=0}^m {[\phi_k(x)]^2\over\gamma_k}=-{A_m\phi_m'(x_i)\phi_{m+1}(x_i)\over A_{m+1}\gamma_m}={1\over w_i}
\end{displaymath}](g_1065.gif) |
(13) |
In the Notation of Szegö (1975), let
![]() be an ordered set of points in
be an ordered set of points in ![]() , and let
, and let
![]() , ...,
, ..., ![]() be a set of Real Numbers.
If
be a set of Real Numbers.
If ![]() is an arbitrary function on the Closed Interval
is an arbitrary function on the Closed Interval ![]() , write
the Mechanical Quadrature as
, write
the Mechanical Quadrature as
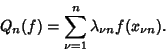 |
(14) |
See also Chebyshev Quadrature, Chebyshev-Gauss Quadrature, Chebyshev-Radau Quadrature, Fundamental Theorem of Gaussian Quadrature, Hermite-Gauss Quadrature, Jacobi-Gauss Quadrature, Laguerre-Gauss Quadrature, Legendre-Gauss Quadrature, Lobatto Quadrature, Mehler Quadrature, Radau Quadrature
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 887-888, 1972.
Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., p. 103, 1990.
Arfken, G. ``Appendix 2: Gaussian Quadrature.'' Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 968-974, 1985.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 461, 1987.
Chandrasekhar, S. An Introduction to the Study of Stellar Structure. New York: Dover, 1967.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 319-323, 1956.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Gaussian Quadratures and Orthogonal Polynomials.'' §4.5 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 140-155, 1992.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 37-48 and 340-349, 1975.
Whittaker, E. T. and Robinson, G. The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed.
New York: Dover, pp. 152-163, 1967.
|
|
|
© 1996-9 Eric W. Weisstein