|
|
|
Also called Jacobi Quadrature or Mehler Quadrature. A Gaussian Quadrature over the interval ![]() with Weighting Function
with Weighting Function
![]() . The Abscissas for quadrature order
. The Abscissas for quadrature order ![]() are given by the roots of the Jacobi Polynomials
are given by the roots of the Jacobi Polynomials
![]() . The weights are
. The weights are
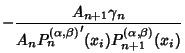 |
|||
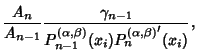 |
(1) |
| (2) |
| (3) |
 |
(4) | ||
![$\displaystyle {\Gamma(n+\alpha+1)\Gamma(n+\beta+1)\over\Gamma(n+\alpha+\beta+1)}
{2^{2n+\alpha+\beta+1}n!\over(1-{x_i}^2)[V_n'(x_i)]^2},$](j_246.gif) |
(5) |
| (6) |
| (7) |
References
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 331-334, 1956.