|
|
|
Also known as the Hypergeometric Polynomials, they occur in the study of
Rotation Groups and in the solution to the equations of motion of the symmetric
top. ![]() They are solutions to the Jacobi Differential Equation. Plugging
They are solutions to the Jacobi Differential Equation. Plugging
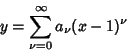 |
(1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Jacobi polynomials are Orthogonal satisfying
| (9) |
| (10) |
|
|
|
|
|
|
|
|
(11) |
| (12) |
The Derivative is given by
| (13) |
The Orthogonal Polynomials with Weighting Function
![]() on the
Closed Interval
on the
Closed Interval ![]() can be expressed in the form
can be expressed in the form
| (14) |
Special cases with ![]() are
are
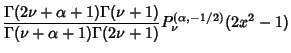 |
(15) | ||
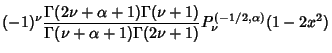 |
(16) | ||
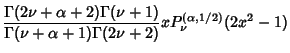 |
(17) | ||
 |
(18) |
Further identities are
| (19) |
| (20) |
|
|
|

|
(21) |
The Kernel Polynomial is
|
|
|
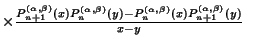
|
(22) |
The Discriminant is
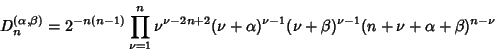 |
(23) |
For
![]() ,
,
![]() reduces to a Legendre Polynomial. The Gegenbauer Polynomial
reduces to a Legendre Polynomial. The Gegenbauer Polynomial
| (24) |
| (25) |
| (26) |
Let ![]() be the number of zeros in
be the number of zeros in ![]() ,
, ![]() the number of zeros in
the number of zeros in
![]() , and
, and ![]() the
number of zeros in
the
number of zeros in
![]() . Define Klein's symbol
. Define Klein's symbol
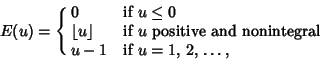 |
(27) |
| (28) | |||
| (29) | |||
| (30) |
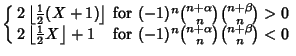 |
(31) | ||
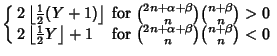 |
(32) | ||
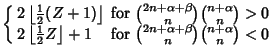 |
(33) |
The first few Polynomials are
| (34) | |||
| (35) | |||
| (36) |
See also Chebyshev Polynomial of the First Kind, Gegenbauer Polynomial, Jacobi Function of the Second Kind, Rising Factorial, Zernike Polynomial
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 771-802, 1972.
Iyanaga, S. and Kawada, Y. (Eds.). ``Jacobi Polynomials.'' Appendix A, Table 20.V in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1480, 1980.
Szegö, G. ``Jacobi Polynomials.'' Ch. 4 in Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.
|
|
|
© 1996-9 Eric W. Weisstein