|
|
|
The number of ways of picking ![]() unordered outcomes from
unordered outcomes from ![]() possibilities. Also known as a Combination. The
binomial coefficients form the rows of Pascal's Triangle. The symbols
possibilities. Also known as a Combination. The
binomial coefficients form the rows of Pascal's Triangle. The symbols ![]() and
and
| (1) |
For Positive integer ![]() , the Binomial Theorem gives
, the Binomial Theorem gives
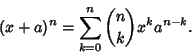 |
(2) |
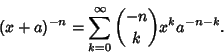 |
(3) |
 |
(4) |
The binomial coefficients satisfy the identities:
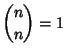 |
(5) | ||
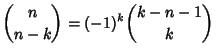 |
(6) | ||
 |
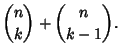 |
(7) |
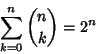 |
(8) |
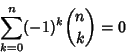 |
(9) |
 |
(10) |
 |
(11) |
|
|
|
|
|
(12) |
 |
(13) |
![\begin{displaymath}
\sum_{k=0}^n {n+k\choose k}[x^{n+1}(1-x)^k+(1-x)^{n+1}x^k]=1
\end{displaymath}](b_1298.gif) |
(14) |
Recurrence Relations of the sums
 |
(15) |
| (16) |
| (17) |
| (18) |
|
|
|
|
|
(19) |
A fascinating series of identities involving binomial coefficients times small powers are
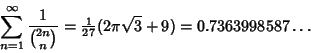 |
(20) |
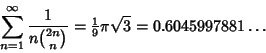 |
(21) |
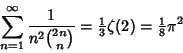 |
(22) |
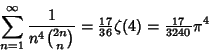 |
(23) |
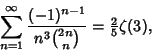 |
(24) |
As shown by Kummer ![]() in 1852, the exact Power of
in 1852, the exact Power of ![]() dividing
dividing
![]() is equal to
is equal to
| (25) |
| (26) |
R. W. Gosper showed that
| (27) |
Consider the binomial coefficients
![]() , the first few of which are 1, 3, 10, 35, 126, ... (Sloane's A001700).
The Generating Function is
, the first few of which are 1, 3, 10, 35, 126, ... (Sloane's A001700).
The Generating Function is
| (28) |
The binomial coefficients
![]() are called Central Binomial Coefficients, where
are called Central Binomial Coefficients, where
![]() is the Floor Function, although the subset of coefficients
is the Floor Function, although the subset of coefficients ![]() is sometimes
also given this name. Erdös and Graham (1980, p. 71) conjectured that the Central Binomial Coefficient
is sometimes
also given this name. Erdös and Graham (1980, p. 71) conjectured that the Central Binomial Coefficient ![]() is never Squarefree for
is never Squarefree for ![]() , and this is sometimes known as the Erdös Squarefree Conjecture. Sárközy's Theorem (Sárközy 1985) provides a partial solution which
states that the Binomial Coefficient
, and this is sometimes known as the Erdös Squarefree Conjecture. Sárközy's Theorem (Sárközy 1985) provides a partial solution which
states that the Binomial Coefficient ![]() is never Squarefree for all sufficiently large
is never Squarefree for all sufficiently large ![]() (Vardi 1991). Granville and Ramare (1996) proved that the only Squarefree values are
(Vardi 1991). Granville and Ramare (1996) proved that the only Squarefree values are ![]() and 4. Sander (1992)
subsequently showed that
and 4. Sander (1992)
subsequently showed that
![]() are also never Squarefree for sufficiently large
are also never Squarefree for sufficiently large ![]() as long as
as long as ![]() is not
``too big.''
is not
``too big.''
For ![]() ,
, ![]() , and
, and ![]() distinct Primes, then the above function satisfies
distinct Primes, then the above function satisfies
| (29) |
The binomial coefficient ![]() mod 2 can be computed using the XOR operation
mod 2 can be computed using the XOR operation ![]() XOR
XOR ![]() , making Pascal's
Triangle mod 2 very easy to construct.
, making Pascal's
Triangle mod 2 very easy to construct.

The binomial coefficient ``function'' can be defined as
| (30) |
See also Ballot Problem, Binomial Distribution, Binomial Theorem, Central Binomial Coefficient, Chu-Vandermonde Identity, Combination, Deficiency, Erdös Squarefree Conjecture, Gaussian Coefficient, Gaussian Polynomial, Kings Problem, Multinomial Coefficient, Permutation, Roman Coefficient, Sárközy's Theorem, Strehl Identity, Wolstenholme's Theorem
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Binomial Coefficients.'' §24.1.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 10 and 822-823, 1972.
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Amsterdam, Netherlands: Kluwer, 1974.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 66-74, 1996.
Erdös, P.; Graham, R. L.; Nathanson, M. B.; and Jia, X.
Old and New Problems and Results in Combinatorial Number Theory. New York: Springer-Verlag, 1998.
Fowler, D. ``The Binomial Coefficient Function.'' Amer. Math. Monthly 103, 1-17, 1996.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. ``Binomial Coefficients.'' Ch. 5 in
Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, pp. 153-242, 1990.
Granville, A. and Ramare, O. ``Explicit Bounds on Exponential Sums and the Scarcity of Squarefree Binomial Coefficients.''
Mathematika 43, 73-107, 1996.
Guy, R. K. ``Binomial Coefficients,'' ``Largest Divisor of a Binomial Coefficient,'' and ``Series Associated with
the
Harborth, H. ``Number of Odd Binomial Coefficients.'' Not. Amer. Math. Soc. 23, 4, 1976.
Hilton, P. and Pedersen, J. ``Catalan Numbers, Their Generalization, and Their Uses.'' Math. Intel. 13, 64-75, 1991.
Jutila, M. ``On Numbers with a Large Prime Factor.'' J. Indian Math. Soc. 37, 43-53, 1973.
Jutila, M. ``On Numbers with a Large Prime Factor. II.'' J. Indian Math. Soc. 38, 125-130, 1974.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.
Ogilvy, C. S. ``The Binomial Coefficients.'' Amer. Math. Monthly 57, 551-552, 1950.
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, 1996.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Gamma Function, Beta Function, Factorials,
Binomial Coefficients.'' §6.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed.
Cambridge, England: Cambridge University Press, pp. 206-209, 1992.
Prudnikov, A. P.; Marichev, O. I.; and Brychkow, Yu. A. Formula 41 in Integrals and Series, Vol. 1: Elementary Functions.
Newark, NJ: Gordon & Breach, p. 611, 1986.
Ribenboim, P. The Book of Prime Number Records, 2nd ed. New York: Springer-Verlag, pp. 23-24, 1989.
Riordan, J. ``Inverse Relations and Combinatorial Identities.'' Amer. Math. Monthly 71, 485-498, 1964.
Sander, J. W. ``On Prime Divisors of Binomial Coefficients.'' Bull. London Math. Soc. 24, 140-142, 1992.
Sárközy, A. ``On the Divisors of Binomial Coefficients, I.'' J. Number Th. 20, 70-80, 1985.
Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica.
Reading, MA: Addison-Wesley, p. 262, 1990.
Sloane, N. J. A. Sequences
A046097 and
A001700/M2848
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Spanier, J. and Oldham, K. B. ``The Binomial Coefficients
Sved, M. ``Counting and Recounting.'' Math. Intel. 5, 21-26, 1983.
Vardi, I. ``Application to Binomial Coefficients,'' ``Binomial Coefficients,'' ``A Class of Solutions,''
``Computing Binomial Coefficients,'' and ``Binomials Modulo and Integer.''
§2.2, 4.1, 4.2, 4.3, and 4.4 in Computational Recreations in Mathematica.
Redwood City, CA: Addison-Wesley, pp. 25-28 and 63-71, 1991.
Wolfram, S. ``Geometry of Binomial Coefficients.'' Amer. Math. Monthly 91, 566-571, 1984.
![]() -Function.'' §B31, B33, and F17 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 84-85, 87-89, and 257-258, 1994.
-Function.'' §B31, B33, and F17 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 84-85, 87-89, and 257-258, 1994.
![]() .''
Ch. 6 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 43-52, 1987.
.''
Ch. 6 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 43-52, 1987.
|
|
|
© 1996-9 Eric W. Weisstein