|
|
|
A prime number is a Positive Integer ![]() which has no Divisors other than 1 and
which has no Divisors other than 1 and ![]() itself.
Although the number 1 used to be considered a prime, it requires special treatment in so many definitions and applications
involving primes greater than or equal to 2 that it is usually placed into a class of its own. Since 2 is the only Even
prime, it is also somewhat special, so the set of all primes excluding 2 is called the ``Odd Primes.''
The first few primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, ... (Sloane's A000040, Hardy and Wright 1979, p. 3).
Positive Integers other than 1 which are not prime are called Composite.
itself.
Although the number 1 used to be considered a prime, it requires special treatment in so many definitions and applications
involving primes greater than or equal to 2 that it is usually placed into a class of its own. Since 2 is the only Even
prime, it is also somewhat special, so the set of all primes excluding 2 is called the ``Odd Primes.''
The first few primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, ... (Sloane's A000040, Hardy and Wright 1979, p. 3).
Positive Integers other than 1 which are not prime are called Composite.
The function which gives the number of primes less than a number ![]() is denoted
is denoted ![]() and is called the Prime
Counting Function. The theorem giving an asymptotic form for
and is called the Prime
Counting Function. The theorem giving an asymptotic form for ![]() is called the Prime Number Theorem.
is called the Prime Number Theorem.
Prime numbers can be generated by sieving processes (such as the Eratosthenes Sieve), and Lucky Numbers, which are also generated by sieving, appear to share some interesting asymptotic properties with the primes.
Many Prime Factorization Algorithms have been devised for determining the prime factors of a given Integer. They vary quite a bit in sophistication and complexity. It is very difficult to build a general-purpose algorithm for this computationally ``hard'' problem, so any additional information which is known about the number in question or its factors can often be used to save a large amount of time. The simplest method of finding factors is so-called ``Direct Search Factorization'' (a.k.a. Trial Division). In this method, all possible factors are systematically tested using trial division to see if they actually Divide the given number. It is practical only for very small numbers.
Because of their importance in encryption algorithms such as RSA Encryption, prime numbers can be important commercial commodities. In fact, Roger Schlafly has obtained U.S. Patent 5,373,560 (12/13/94) on the following two primes (expressed in hexadecimal notation):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The Fundamental Theorem of Arithmetic states that any Positive Integer can be represented in exactly one
way as a Product of primes. Euclid's Second Theorem demonstrated that there
are an infinite number of primes. However, it is not known if there are an infinite number of primes of the form
![]() , whether there are an Infinite number of Twin Primes, or if a prime can always be found between
, whether there are an Infinite number of Twin Primes, or if a prime can always be found between
![]() and
and ![]() .
.
Prime numbers satisfy many strange and wonderful properties. For example, there exists a Constant
![]() known as Mills' Constant such that
known as Mills' Constant such that
| (1) |
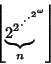 |
(2) |
Explicit Formulas exist for the ![]() th prime both as a function of
th prime both as a function of ![]() and in terms of the primes 2,
...,
and in terms of the primes 2,
..., ![]() (Hardy and Wright 1979, pp. 5-6; Guy 1994, pp. 36-41). Let
(Hardy and Wright 1979, pp. 5-6; Guy 1994, pp. 36-41). Let
| (3) |
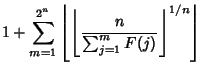 |
(4) | ||
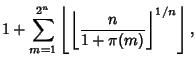 |
(5) |
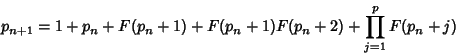 |
(6) |
![$\displaystyle {2\over\prod_{i=n}^\infty \left[{1+{\sin({\textstyle{1\over 2}}\pi p_n)\over p_n}}\right]}$](p3_650.gif) |
(7) | ||
![$\displaystyle {2\over\prod_{i=n}^\infty \left[{1+{(-1)^{(p_n-1)/2}\over p_n}}\right]}$](p3_651.gif) |
(8) |
Some curious identities satisfied by primes ![]() are
are
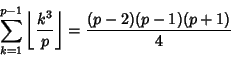 |
(9) |
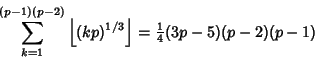 |
(10) |
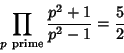 |
(11) |
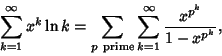 |
(12) |
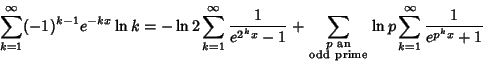 |
(13) |
It has been proven that the set of prime numbers is a Diophantine Set (Ribenboim 1991, pp. 106-107).
Ramanujan ![]() also showed that
also showed that
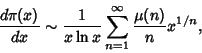 |
(14) |
| (15) |
| (16) |
| (17) |
| (18) | |||
| (19) | |||
| (20) |
| (21) |
Cheng (1979) showed that for ![]() sufficiently large, there always exist at least two prime factors between
sufficiently large, there always exist at least two prime factors between ![]() and
and
![]() for
for
![]() (Le Lionnais 1983, p. 26). Let
(Le Lionnais 1983, p. 26). Let ![]() be the number of decompositions of
be the number of decompositions of ![]() into two or more
consecutive primes. Then
into two or more
consecutive primes. Then
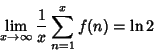 |
(22) |
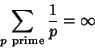 |
(23) |
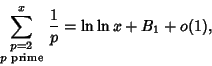 |
(24) |
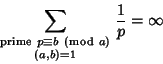 |
(25) |
Despite the fact that ![]() diverges, Brun showed that
diverges, Brun showed that
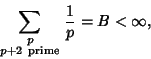 |
(26) |
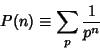 |
(27) |
The probability that the largest prime factor of a Random Number ![]() is less than
is less than ![]() is ln 2 (Beeler et al. 1972,
Item 29). The probability that two Integers picked at random are Relatively Prime is
is ln 2 (Beeler et al. 1972,
Item 29). The probability that two Integers picked at random are Relatively Prime is
![]() , where
, where ![]() is the Riemann Zeta Function (Cesaro and Sylvester 1883). Given three
Integers chosen at random, the probability that no common factor will divide them all is
is the Riemann Zeta Function (Cesaro and Sylvester 1883). Given three
Integers chosen at random, the probability that no common factor will divide them all is
| (28) |
Large primes include the large Mersenne Primes, Ferrier's Prime, and
![]() (Cipra 1989). The largest known prime as of 1998, is the Mersenne Prime
(Cipra 1989). The largest known prime as of 1998, is the Mersenne Prime ![]() .
.
Primes consisting of consecutive Digits (counting 0 as coming after 9) include 2, 3, 5, 7, 23, 67, 89, 4567, 78901, ... (Sloane's A006510).
See also Adleman-Pomerance-Rumely Primality Test, Almost Prime, Andrica's Conjecture, Bertrand's Postulate, Brocard's Conjecture, Brun's Constant, Carmichael's Conjecture, Carmichael Function, Carmichael Number, Chebyshev Function, Chebyshev-Sylvester Constant, Chen's Theorem, Chinese Hypothesis, Composite Number, Composite Runs, Copeland-Erdös Constant, Cramer Conjecture, Cunningham Chain, Cyclotomic Polynomial, de Polignac's Conjecture, Dirichlet's Theorem, Divisor, Erdös-Kac Theorem, Euclid's Theorems, Feit-Thompson Conjecture, Fermat Number, Fermat Quotient, Ferrier's Prime, Fortunate Prime, Fundamental Theorem of Arithmetic, Gigantic Prime, Giuga's Conjecture, Goldbach Conjecture, Good Prime, Grimm's Conjecture, Hardy-Ramanujan Theorem, Irregular Prime, Kummer's Conjecture, Lehmer's Problem, Linnik's Theorem, Long Prime, Mersenne Number, Mertens Function, Miller's Primality Test, Mirimanoff's Congruence, Möbius Function, Palindromic Number, Pépin's Test, Pillai's Conjecture, Poulet Number, Primary, Prime Array, Prime Circle, Prime Factorization Algorithms, Prime Number of Measurement, Prime Number Theorem, Prime Power Symbol, Prime String, Prime Triangle, Prime Zeta Function, Primitive Prime Factor, Primorial, Probable Prime, Pseudoprime, Regular Prime, Riemann Function, Rotkiewicz Theorem, Schnirelmann's Theorem, Selfridge's Conjecture, Semiprime, Shah-Wilson Constant, Sierpinski's Composite Number Theorem, Sierpinski's Prime Sequence Theorem, Smooth Number, Soldner's Constant, Sophie Germain Prime, Titanic Prime, Totient Function, Totient Valence Function, Twin Primes, Twin Primes Constant, Vinogradov's Theorem, von Mangoldt Function, Waring's Conjecture, Wieferich Prime, Wilson Prime, Wilson Quotient, Wilson's Theorem, Witness, Wolstenholme's Theorem, Zsigmondy Theorem
References
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Berndt, B. C. ``Ramanujan's Theory of Prime Numbers.'' Ch. 24 in Ramanujan's Notebooks, Part IV.
New York: Springer-Verlag, 1994.
Blatner, D. The Joy of Pi. New York: Walker, p. 110, 1997.
Caldwell, C. ``Largest Primes.'' http://www.utm.edu/research/primes/largest.html.
Cheng, J. R. ``On the Distribution of Almost Primes in an Interval II.'' Sci. Sinica 22, 253-275, 1979.
Cipra, B. A. ``Math Team Vaults Over Prime Record.'' Science 245, 815, 1989.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 130, 1996.
Courant, R. and Robbins, H. ``The Prime Numbers.'' §1 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 21-31, 1996.
Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, 1980.
Deutsch, E. ``Problem 1494.'' Math. Mag. 69, 143, 1996.
Dickson, L. E. ``Factor Tables, Lists of Primes.'' Ch. 13 in
History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 347-356, 1952.
Doster, D. Problem 10346. Amer. Math. Monthly 100, 951, 1993.
Giblin, P. J. Primes and Programming: Computers and Number Theory. New York: Cambridge University Press, 1994.
Guy, R. K. ``Conway's Prime Producing Machine.'' Math. Mag. 56, 26-33, 1983.
Guy, R. K. ``Prime Numbers,'' ``Formulas for Primes,'' and ``Products Taken Over Primes.''
Ch. A, §A17, and §B48 in Unsolved Problems in Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 3-43, 36-41 and 102-103, 1994.
Hardy, G. H. Ch. 2 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed.
New York: Chelsea, 1978.
Hardy, G. H. and Wright, E. M. ``Prime Numbers'' and ``The Sequence of Primes.'' §1.2 and 1.4 in
An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 1-4, 1979.
Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., p. 30, 1976.
Kraitchik, M. ``Prime Numbers.'' §3.9 in Mathematical Recreations. New York: W. W. Norton, pp. 78-79, 1942.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 26, 30, and 46, 1983.
Moser, L. ``Notes on Number Theory III. On the Sum of Consecutive Primes.'' Can. Math. Bull. 6, 159-161, 1963.
Pappas, T. ``Prime Numbers.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 100-101, 1989.
Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, 1991.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, 1994.
Schinzel, A. and Sierpinski, W. ``Sur certains hypothèses concernant les nombres premiers.'' Acta Arith. 4, 185-208, 1958.
Schinzel, A. and Sierpinski, W. Erratum to ``Sur certains hypothèses concernant les nombres premiers.'' Acta Arith. 5, 259, 1959.
Sloane, N. J. A. Sequences
A046024,
A000040/M0652, and
A006510/M0679,
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Wagon, S. ``Primes Numbers.'' Ch. 1 in Mathematica in Action. New York: W. H. Freeman, pp. 11-37, 1991.
Zaiger, D. ``The First 50 Million Prime Numbers.'' Math. Intel. 0, 221-224, 1977.
![]() Prime Numbers
Prime Numbers
|
|
|
© 1996-9 Eric W. Weisstein