Goldbach Conjecture

Goldbach's original conjecture, written in a 1742 letter to Euler, states that every Integer $>5$ is the Sum of three Primes. As re-expressed by Euler, an equivalent of this Conjecture (called the ``strong'' Goldbach conjecture) asserts that all Positive Even Integers $\geq 4$ can be expressed as the Sum of two Primes. Schnirelmann (1931) proved that every Even number can be written as the sum of not more than 300,000 Primes (Dunham 1990), which seems a rather far cry from a proof for two Primes! The strong Goldbach conjecture has been shown to be true up to $4\times 10^{11}$ by Sinisalo (1993). Pogorzelski (1977) claimed to have proven the Goldbach conjecture, but his proof is not generally accepted (Shanks 1993).

The conjecture that all Odd numbers $\geq 9$ are the Sum of three Odd Primes is called the ``weak'' Goldbach conjecture. Vinogradov proved that all Odd Integers starting at some sufficiently large value are the Sum of three Primes (Guy 1994). The original ``sufficiently large'' $N\geq 3^{3^{15}}=e^{e^{16.573}}$ was subsequently reduced to $e^{e^{11.503}}$ by Chen and Wang (1989). Chen (1973, 1978) also showed that all sufficiently large Even Numbers are the sum of a Prime and the Product of at most two Primes (Guy 1994, Courant and Robbins 1996).

It has been shown that if the weak Goldbach conjecture is false, then there are only a Finite number of exceptions.

Other variants of the Goldbach conjecture include the statements that every Even number $\geq 6$ is the Sum of two Odd Primes, and every Integer $>17$ the sum of exactly three distinct Primes. Let $R(n)$ be the number of representations of an Even Integer $n$ as the sum of two Primes. Then the ``extended'' Goldbach conjecture states that

$$R(n)\sim 2\Pi_2 \prod_{\scriptstyle k=2\atop\scriptstyle p_k\vert n} {p_k-1\over p_k-2} \int_2^x {dx\over (\ln x)^2},$$

where $\Pi_2$ is the Twin Primes Constant (Halberstam and Richert 1974).

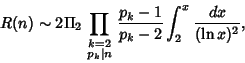
If the Goldbach conjecture is true, then for every number $m$, there are Primes $p$ and $q$ such that

$$\phi(p)+\phi(q)=2m,$$

where $\phi(x)$ is the Totient Function (Guy 1994, p. 105).

Vinogradov (1937ab, 1954) proved that every sufficiently large Odd Number is the sum of three Primes, and Estermann (1938) proves that almost all Even Numbers are the sums of two Primes.

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 64, 1987.

Chen, J.-R. ``On the Representation of a Large Even Number as the Sum of a Prime and the Product of at Most Two Primes.'' Sci. Sinica 16, 157-176, 1973.

Chen, J.-R. ``On the Representation of a Large Even Number as the Sum of a Prime and the Product of at Most Two Primes, II.'' Sci. Sinica 21, 421-430, 1978.

Chen, J.-R. and Wang, T.-Z. ``On the Goldbach Problem.'' Acta Math. Sinica 32, 702-718, 1989.

Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 30-31, 1996.

Devlin, K. Mathematics: The New Golden Age. London: Penguin Books, 1988.

Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, p. 83, 1990.

Estermann, T. ``On Goldbach's Problem: Proof that Almost All Even Positive Integers are Sums of Two Primes.'' Proc. London Math. Soc. Ser. 2 44, 307-314, 1938.

Guy, R. K. ``Goldbach's Conjecture.'' §C1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 105-107, 1994.

Hardy, G. H. and Littlewood, J. E. ``Some Problems of Partitio Numerorum (V): A Further Contribution to the Study of Goldbach's Problem.'' Proc. London Math. Soc. Ser. 2 22, 46-56, 1924.

Halberstam, H. and Richert, H.-E. Sieve Methods. New York: Academic Press, 1974.

Pogorzelski, H. A. ``Goldbach Conjecture.'' J. Reine Angew. Math. 292, 1-12, 1977.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 30-31 and 222, 1985.

Sinisalo, M. K. ``Checking the Goldbach Conjecture up to $4\cdot 10^{11}$.'' Math. Comput. 61, 931-934, 1993.

Vinogradov, I. M. ``Representation of an Odd Number as a Sum of Three Primes.'' Comtes rendus (Doklady) de l'Académie des Sciences de l'U.R.S.S. 15, 169-172, 1937a.

Vinogradov, I. ``Some Theorems Concerning the Theory of Primes.'' Recueil Math. 2, 179-195, 1937b.

Vinogradov, I. M. The Method of Trigonometrical Sums in the Theory of Numbers. London: Interscience, p. 67, 1954.

Yuan, W. Goldbach Conjecture. Singapore: World Scientific, 1984.