|
|
|
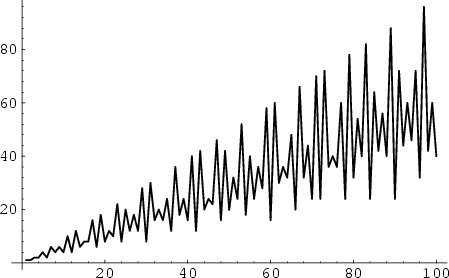
The totient function ![]() , also called Euler's totient function, is defined as the number of Positive
Integers
, also called Euler's totient function, is defined as the number of Positive
Integers ![]() which are Relatively Prime to (i.e., do not contain any factor in common with)
which are Relatively Prime to (i.e., do not contain any factor in common with)
![]() , where 1 is counted as being Relatively Prime to all numbers. Since a number less than or equal to and
Relatively Prime to a given number is called a Totative, the totient function
, where 1 is counted as being Relatively Prime to all numbers. Since a number less than or equal to and
Relatively Prime to a given number is called a Totative, the totient function ![]() can be simply defined
as the number of Totatives of
can be simply defined
as the number of Totatives of ![]() . For example, there are eight Totatives of 24 (1,
5, 7, 11, 13, 17, 19, and 23), so
. For example, there are eight Totatives of 24 (1,
5, 7, 11, 13, 17, 19, and 23), so ![]() .
.
By convention, ![]() . The first few values of
. The first few values of ![]() for
for ![]() , 2, ... are 1, 1, 2, 2, 4, 2, 6, 4, 6,
4, 10, ... (Sloane's A000010).
, 2, ... are 1, 1, 2, 2, 4, 2, 6, 4, 6,
4, 10, ... (Sloane's A000010). ![]() is plotted above for small
is plotted above for small ![]() .
.
For a Prime ![]() ,
,
| (1) |
| (2) |
| (3) |
| (4) |
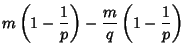 |
|||
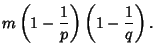 |
(5) |
| (6) |
| (7) |
| (8) |
The Divisor Function satisfies the Congruence
| (9) |
| (10) |
Walfisz (1963), building on the work of others, showed that
![\begin{displaymath}
\sum_{n=1}^N \phi(n) ={3N^2\over\pi^2}+{\mathcal O}[N(\ln N)^{2/3}(\ln\ln N)^{4/3}],
\end{displaymath}](t_991.gif) |
(11) |
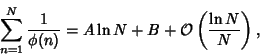 |
(12) |
![$\displaystyle \sum_{k=1}^\infty {[\mu(k)]^2\over k\phi(k)}={\zeta(2)\zeta(3)\over\zeta(6)}={315\over 2\pi^4}\zeta(3)$](t_993.gif) |
|||
| (13) | |||
![$\displaystyle \gamma {315\over 2\pi^4}\zeta(3)-\sum_{k=1}^\infty {[\mu(k)]^2\ln k\over k\phi(k)}$](t_995.gif) |
|||
| (14) |
![\begin{displaymath}
A=\prod_{k=1}^\infty {1-{p_k}^6\over (1-{p_k}^{-2})(1-{p_k}^...
...)}
= \prod_{k=1}^\infty \left[{1+{1\over p_k(p_k-1)}}\right].
\end{displaymath}](t_999.gif) |
(15) |
If the Goldbach Conjecture is true, then for every number ![]() , there are Primes
, there are Primes ![]() and
and ![]() such that
such that
| (16) |
Curious equalities of consecutive values include
| (17) |
| (18) |
| (19) |
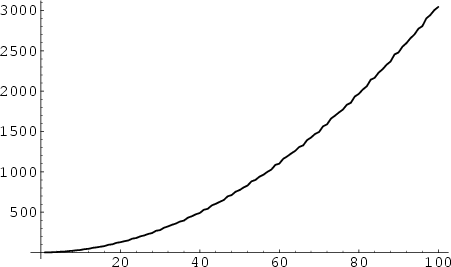
The Summatory totient function, plotted above, is defined by
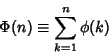 |
(20) |
| (21) | |||
| (22) |
See also Dedekind Function, Euler's Totient Rule, Fermat's Little Theorem, Lehmer's Problem, Leudesdorf Theorem, Noncototient, Nontotient, Silverman Constant, Totative, Totient Valence Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``The Euler Totient Function.'' §24.3.2 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 826, 1972.
Beiler, A. H. Ch. 12 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York:
Dover, 1966.
Conway, J. H. and Guy, R. K. ``Euler's Totient Numbers.'' The Book of Numbers. New York:
Springer-Verlag, pp. 154-156, 1996.
Courant, R. and Robbins, H. ``Euler's
DeKoninck, J.-M. and Ivic, A.
Topics in Arithmetical Functions: Asymptotic Formulae for Sums of Reciprocals of Arithmetical Functions and Related Fields.
Amsterdam, Netherlands: North-Holland, 1980.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 113-158, 1952.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/totient/totient.html
Guy, R. K. ``Euler's Totient Function,'' ``Does
Halberstam, H. and Richert, H.-E. Sieve Methods. New York: Academic Press, 1974.
Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., p. 35, 1976.
Perrot, J. 1811. Quoted in Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality.
New York: Chelsea, p. 126, 1952.
Shanks, D. ``Euler's
Sloane, N. J. A. Sequences
A000010/M0299
and A002088/M1008
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Subbarao, M. V. ``On Two Congruences for Primality.'' Pacific J. Math. 52, 261-268, 1974.
![]() Function. Fermat's Theorem Again.'' §2.4.3 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 48-49, 1996.
Function. Fermat's Theorem Again.'' §2.4.3 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 48-49, 1996.
![]() Properly Divide
Properly Divide ![]() ,'' ``Solutions of
,'' ``Solutions of
![]() ,''
``Carmichael's Conjecture,'' ``Gaps Between Totatives,'' ``Iterations of
,''
``Carmichael's Conjecture,'' ``Gaps Between Totatives,'' ``Iterations of ![]() and
and ![]() ,''
``Behavior of
,''
``Behavior of
![]() and
and
![]() .'' §B36-B42 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 90-99, 1994.
.'' §B36-B42 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 90-99, 1994.
![]() Function.'' §2.27 in Solved and Unsolved Problems in Number Theory, 4th ed.
New York: Chelsea, pp. 68-71, 1993.
Function.'' §2.27 in Solved and Unsolved Problems in Number Theory, 4th ed.
New York: Chelsea, pp. 68-71, 1993.
|
|
|
© 1996-9 Eric W. Weisstein