|
|
|
If ![]() is integrally divisible by
is integrally divisible by ![]() , then
, then ![]() and
and ![]() are said to be congruent with Modulus
are said to be congruent with Modulus ![]() . This is written mathematically as
. This is written mathematically as ![]() (mod
(mod ![]() ). If
). If ![]() is not divisible by
is not divisible by ![]() , then we
say
, then we
say ![]() (mod
(mod ![]() ). The (mod
). The (mod ![]() ) is sometimes omitted when the Modulus
) is sometimes omitted when the Modulus ![]() is
understood for a given computation, so care must be taken not to confuse the symbol
is
understood for a given computation, so care must be taken not to confuse the symbol ![]() with that for an
Equivalence. The quantity
with that for an
Equivalence. The quantity ![]() is called the Residue or
Remainder. The Common Residue is taken to be Nonnegative and smaller than
is called the Residue or
Remainder. The Common Residue is taken to be Nonnegative and smaller than ![]() , and the Minimal
Residue is
, and the Minimal
Residue is ![]() or
or ![]() , whichever is smaller in Absolute Value. In many computer languages (such as FORTRAN or
Mathematica
, whichever is smaller in Absolute Value. In many computer languages (such as FORTRAN or
Mathematica
![]() ), the Common Residue of
), the Common Residue of ![]() (mod
(mod ![]() ) is written mod(c,a).
) is written mod(c,a).
Congruence arithmetic is perhaps most familiar as a generalization of the arithmetic of the clock: 40 minutes past the hour
plus 35 minutes gives
![]() , or 15 minutes past the hour, and 10 o'clock a.m. plus five hours gives
, or 15 minutes past the hour, and 10 o'clock a.m. plus five hours gives
![]() , or 3 o'clock p.m. Congruences satisfy a number of important properties, and are extremely useful in
many areas of Number Theory. Using congruences, simple Divisibility Tests to check whether a given number is
divisible by another number can sometimes be derived. For example, if the sum of a number's digits is divisible by 3 (9),
then the original number is divisible by 3 (9).
, or 3 o'clock p.m. Congruences satisfy a number of important properties, and are extremely useful in
many areas of Number Theory. Using congruences, simple Divisibility Tests to check whether a given number is
divisible by another number can sometimes be derived. For example, if the sum of a number's digits is divisible by 3 (9),
then the original number is divisible by 3 (9).
Congruences also have their limitations. For example, if ![]() and
and
![]() , then it follows that
, then it follows that ![]() , but usually not that
, but usually not that ![]() or
or ![]() . In addition, by ``rolling over,'' congruences discard
absolute information. For example, knowing the number of minutes past the hour is useful, but knowing the hour the minutes
are past is often more useful still.
. In addition, by ``rolling over,'' congruences discard
absolute information. For example, knowing the number of minutes past the hour is useful, but knowing the hour the minutes
are past is often more useful still.
Let
![]() and
and
![]() , then important properties of congruences include the following, where
, then important properties of congruences include the following, where ![]() means
``Implies'':
means
``Implies'':
Properties (6-8) can be proved simply by defining
| (1) | |||
| (2) |
| (3) | |||
| (4) | |||
| (5) |
Congruences also apply to Fractions. For example, note that
| (6) |
| (7) |
| (8) |
| (9) |
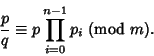 |
(10) |
| (11) |
| (12) |
A general Quadratic Congruence
| (13) |
| (14) |
| (15) |
Two simultaneous congruences
| (16) |
| (17) |
| (18) |
See also Cancellation Law, Chinese Remainder Theorem, Common Residue, Congruence Axioms, Divisibility Tests, Greatest Common Divisor, Least Common Multiple, Minimal Residue, Modulus (Congruence), Quadratic Reciprocity Law, Residue (Congruence)
References
Conway, J. H. and Guy, R. K. ``Arithmetic Modulo
Courant, R. and Robbins, H. ``Congruences.'' §2 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 31-40, 1996.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 55, 1993.
![]() .'' In The Book of Numbers. New York: Springer-Verlag,
pp. 130-132, 1996.
.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 130-132, 1996.
![]() Weisstein, E. W. ``Fractional Congruences.'' Mathematica notebook ModFraction.m.
Weisstein, E. W. ``Fractional Congruences.'' Mathematica notebook ModFraction.m.
|
|
|
© 1996-9 Eric W. Weisstein