|
|
|
An algorithm used to recursively construct a Set of objects from the smallest possible constituent parts.
Given a Set of ![]() Integers (
Integers (![]() ,
, ![]() , ...,
, ..., ![]() ) with
) with
![]() , a greedy
algorithm can be used to find a Vector of coefficients (
, a greedy
algorithm can be used to find a Vector of coefficients (![]() ,
, ![]() , ...,
, ..., ![]() ) such that
) such that
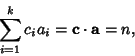 |
(1) |
| (2) |
| (3) |
| (4) |
For example, McNugget Numbers are numbers which are representable using only
![]() . Taking
. Taking ![]() and applying the algorithm iteratively gives the sequence (0, 0, 3), (0, 2, 2), (2, 1, 2), (3,
0, 2), (1, 4, 1), at which point
and applying the algorithm iteratively gives the sequence (0, 0, 3), (0, 2, 2), (2, 1, 2), (3,
0, 2), (1, 4, 1), at which point ![]() . 62 is therefore a McNugget Number with
. 62 is therefore a McNugget Number with
| (5) |
If any Integer ![]() can be represented with
can be represented with ![]() or 1 using a sequence (
or 1 using a sequence (![]() ,
, ![]() , ...), then this sequence
is called a Complete Sequence.
, ...), then this sequence
is called a Complete Sequence.
A greedy algorithm can also be used to break down arbitrary fractions into Unit Fractions in a finite number
of steps. For a Fraction ![]() , find the least Integer
, find the least Integer ![]() such that
such that ![]() , i.e.,
, i.e.,
| (6) |
Paul Erdös and E. G. Strays have conjectured that the Diophantine Equation
| (7) |
| (8) |
See also Complete Sequence, Integer Relation, Levine-O'Sullivan Greedy Algorithm, McNugget Number, Reverse Greedy Algorithm, Square Number, Sylvester's Sequence, Unit Fraction
|
|
|
© 1996-9 Eric W. Weisstein