|
|
|
A vector is a set of numbers ![]() , ...,
, ..., ![]() that transform as
that transform as
| (1) |
A vector is uniquely specified by giving its Divergence and Curl within a region and its normal component
over the boundary, a result known as Helmholtz's Theorem (Arfken 1985, p. 79). A vector from a point ![]() to a point
to a point
![]() is denoted
is denoted
![]() , and a vector
, and a vector ![]() may be denoted
may be denoted ![]() , or more commonly,
, or more commonly, ![]() .
.
A vector with unit length is called a Unit Vector and is denoted with a Hat. An arbitrary vector may be
converted to a Unit Vector by dividing by its Norm, i.e.,
| (2) |
Let ![]() be the Unit Vector defined by
be the Unit Vector defined by
![\begin{displaymath}
\hat{\bf n}\equiv\left[{\matrix{\cos \theta \sin \phi \cr \sin \theta \sin \phi \cr \cos \phi \cr}}\right].
\end{displaymath}](v_360.gif) |
(3) |
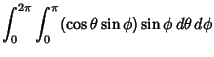 |
|||
![$\displaystyle [\sin \theta]^{2\pi}_0 \int_0^{2\pi} \sin^2\phi \,d\phi =0$](v_363.gif) |
(4) | ||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
| (11) | |||
| (12) | |||
| (13) |
| (14) |
See also Four-Vector, Helmholtz's Theorem, Norm, Pseudovector, Scalar, Tensor, Unit Vector, Vector Field
References
Arfken, G. ``Vector Analysis.'' Ch. 1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 1-84, 1985.
Aris, R. Vectors, Tensors, and the Basic Equations of Fluid Mechanics. New York: Dover, 1989.
Crowe, M. J. A History of Vector Analysis: The Evolution of the Idea of a Vectorial System. New York: Dover, 1985.
Gibbs, J. W. and Wilson, E. B.
Vector Analysis: A Text-Book for the Use of Students of Mathematics and Physics, Founded Upon the Lectures of J. Willard Gibbs.
New York: Dover, 1960.
Marsden, J. E. and Tromba, A. J. Vector Calculus, 4th ed. New York: W. H. Freeman, 1996.
Morse, P. M. and Feshbach, H. ``Vector and Tensor Formalism.'' §1.5 in
Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 44-54, 1953.
Schey, H. M. Div, Grad, Curl, and All That: An Informal Text on Vector Calculus. New York: Norton, 1973.
Schwartz, M.; Green, S.; and Rutledge, W. A. Vector Analysis with Applications to Geometry and Physics.
New York: Harper Brothers, 1960.
Spiegel, M. R. Theory and Problems of Vector Analysis. New York: Schaum, 1959.
![]() Vectors
Vectors
|
|
|
© 1996-9 Eric W. Weisstein