The curl of a Tensor field is given by
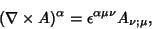 |
(1) |
where
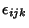 is the Levi-Civita Tensor and ``;'' is the Covariant Derivative. For a Vector
Field, the curl is denoted
is the Levi-Civita Tensor and ``;'' is the Covariant Derivative. For a Vector
Field, the curl is denoted
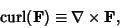 |
(2) |
and
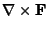 is normal to the Plane in which the ``circulation'' is Maximum. Its magnitude is the
limiting value of circulation per unit Area,
is normal to the Plane in which the ``circulation'' is Maximum. Its magnitude is the
limiting value of circulation per unit Area,
 |
(3) |
Let
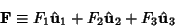 |
(4) |
and
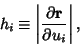 |
(5) |
then
Special cases of the curl formulas above can be given for Curvilinear Coordinates.
See also Curl Theorem, Divergence, Gradient, Vector Derivative
References
Arfken, G. ``Curl, 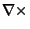 .'' §1.8 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 42-47, 1985.
.'' §1.8 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 42-47, 1985.
© 1996-9 Eric W. Weisstein
1999-05-25
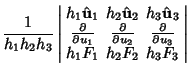
![$\displaystyle {1\over h_2h_3} \left[{{\partial\over \partial u_2}(h_3F_3)- {\partial\over\partial u_3}(h_2F_2)}\right]\hat {\bf u}_1$](c4_488.gif)
![$\displaystyle +{1\over h_1h_3} \left[{{\partial\over \partial u_3}(h_1F_1)-{\partial\over \partial u_1}(h_3F_3)}\right]\hat {\bf u}_2$](c4_489.gif)
![$\displaystyle +{1\over h_1h_2} \left[{{\partial\over \partial u_1}(h_2F_2)- {\partial\over \partial u_2}(h_1F_1)}\right]\hat {\bf u}_3.$](c4_490.gif)
![]() .'' §1.8 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 42-47, 1985.
.'' §1.8 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 42-47, 1985.