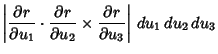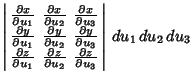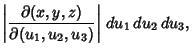A general Metric 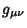 has a Line Element
has a Line Element
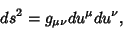 |
(1) |
where Einstein Summation is being used. Curvilinear coordinates are defined as those with a diagonal Metric
so that
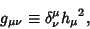 |
(2) |
where
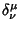 is the Kronecker Delta. Curvilinear coordinates
therefore have a simple Line Element
is the Kronecker Delta. Curvilinear coordinates
therefore have a simple Line Element
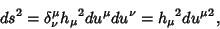 |
(3) |
which is just the Pythagorean Theorem, so the differential Vector
is
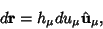 |
(4) |
or
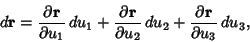 |
(5) |
where the Scale Factors are
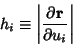 |
(6) |
and
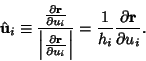 |
(7) |
Equation (5) may therefore be re-expressed as
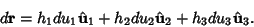 |
(8) |
The Gradient is
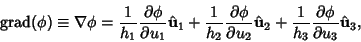 |
(9) |
the Divergence is
![\begin{displaymath}
{\rm div}(F) \equiv \nabla \cdot {\bf F} \equiv {1\over h_1h...
...h_3h_1F_2) + {\partial \over \partial u_3}(h_1h_2F_3)}\right],
\end{displaymath}](c4_632.gif) |
(10) |
and the Curl is
Orthogonal curvilinear coordinates satisfy the additional constraint that
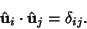 |
(12) |
Therefore, the Line Element is
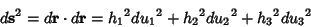 |
(13) |
and the Volume Element is
where the latter is the Jacobian.
Orthogonal curvilinear coordinate systems include Bipolar Cylindrical Coordinates, Bispherical Coordinates,
Cartesian Coordinates, Confocal Ellipsoidal Coordinates, Confocal Paraboloidal Coordinates,
Conical Coordinates, Cyclidic Coordinates, Cylindrical Coordinates, Ellipsoidal Coordinates,
Elliptic Cylindrical Coordinates, Oblate Spheroidal Coordinates, Parabolic Coordinates,
Parabolic Cylindrical Coordinates, Paraboloidal Coordinates, Polar Coordinates, Prolate
Spheroidal Coordinates, Spherical Coordinates, and Toroidal Coordinates. These are degenerate cases of the
Confocal Ellipsoidal Coordinates.
See also Change of Variables Theorem, Curl, Divergence, Gradient, Jacobian,
Laplacian
References
Arfken, G. ``Curvilinear Coordinates'' and ``Differential Vector Operators.'' §2.1 and 2.2 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 86-90 and 90-94, 1985.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, pp. 1084-1088, 1980.
Morse, P. M. and Feshbach, H. ``Curvilinear Coordinates'' and ``Table of Properties of Curvilinear Coordinates.''
§1.3 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 21-31 and 115-117, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() has a Line Element
has a Line Element
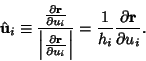
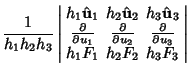
![$\displaystyle {1\over h_2h_3} \left[{{\partial\over \partial u_2}(h_3F_3)- {\partial\over\partial u_3}(h_2F_2)}\right]\hat {\bf u}_1$](c4_488.gif)
![$\displaystyle +{1\over h_1h_3} \left[{{\partial\over \partial u_3}(h_1F_1)-{\partial\over \partial u_1}(h_3F_3)}\right]\hat {\bf u}_2$](c4_489.gif)
![$\displaystyle +{1\over h_1h_2} \left[{{\partial\over \partial u_1}(h_2F_2)- {\partial\over \partial u_2}(h_1F_1)}\right]\hat {\bf u}_3.$](c4_490.gif)