|
|
|
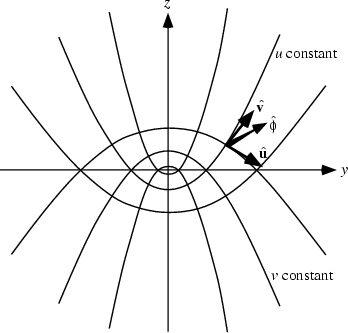
A system of Curvilinear Coordinates in which two sets of coordinate surfaces are obtained by revolving the parabolas
of Parabolic Cylindrical Coordinates about the x-Axis, which is then relabeled the z-Axis. There
are several notational conventions. Whereas
![]() is used in this work,
Arfken (1970) uses
is used in this work,
Arfken (1970) uses
![]() .
.
The equations for the parabolic coordinates are
| (1) | |||
| (2) | |||
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
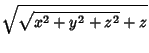 |
(8) | ||
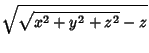 |
(9) | ||
| (10) |
| (11) | |||
| (12) | |||
| (13) |
| (14) |
| (15) |
![$\displaystyle {1\over uv(u^2+v^2)}\left[{{\partial\over\partial u}\left({uv {\p...
...partial v}}\right)}\right]+ {1\over u^2 v^2} {\partial^2f\over\partial\theta^2}$](p1_378.gif) |
|||
![$\displaystyle {1\over u^2+v^2}\left[{{1\over u}{\partial\over\partial u}\left({...
...partial v}}\right)}\right]+ {1\over u^2 v^2} {\partial^2f\over\partial\theta^2}$](p1_379.gif) |
|||
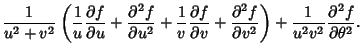 |
(16) |
See also Confocal Paraboloidal Coordinates, Helmholtz Differential Equation--Parabolic Coordinates, Parabolic Cylindrical Coordinates
References
Arfken, G. ``Parabolic Coordinates (
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, p. 660, 1953.
![]() ,
, ![]() ,
, ![]() ).'' §2.12 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 109-112, 1970.
).'' §2.12 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 109-112, 1970.
|
|
|
© 1996-9 Eric W. Weisstein