|
|
|
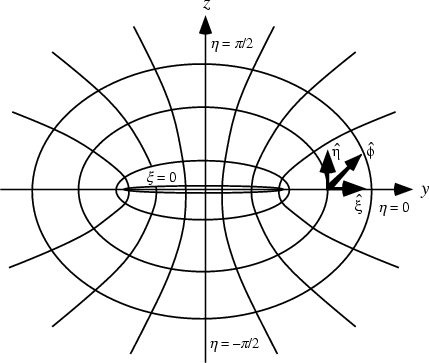
A system of Curvilinear Coordinates in which two sets of coordinate surfaces are obtained by revolving the curves of
the Elliptic Cylindrical Coordinates about the y-Axis which is relabeled the
z-Axis. The third set
of coordinates consists of planes passing through this axis.
| (1) | |||
| (2) | |||
| (3) |
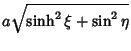 |
(4) | ||
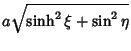 |
(5) | ||
| (6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
|
|
(8) |
An alternate form useful for ``two-center'' problems is defined by
| (9) | |||
| (10) | |||
| (11) | |||
| (12) |
| (13) | |||
 |
(14) | ||
| (15) |
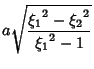 |
(16) | ||
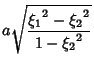 |
(17) | ||
| (18) |
| (19) |
See also Helmholtz Differential Equation--Oblate Spheroidal Coordinates, Latitude, Longitude, Prolate Spheroidal Coordinates, Spherical Coordinates
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Definition of Oblate Spheroidal Coordinates.'' §21.2 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 752, 1972.
Arfken, G. ``Prolate Spheroidal Coordinates (
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 663, 1953.
![]() ,
, ![]() ,
, ![]() ).'' §2.11 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 107-109, 1970.
).'' §2.11 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 107-109, 1970.
|
|
|
© 1996-9 Eric W. Weisstein