|
|
|

A system of Curvilinear Coordinates which is natural for describing positions on a Sphere or Spheroid.
Define ![]() to be the azimuthal Angle in the
to be the azimuthal Angle in the ![]() -Plane from the x-Axis with
-Plane from the x-Axis with
![]() (denoted
(denoted ![]() when referred to as the Longitude),
when referred to as the Longitude), ![]() to be the polar Angle from the z-Axis
with
to be the polar Angle from the z-Axis
with
![]() (Colatitude, equal to
(Colatitude, equal to
![]() where
where ![]() is the Latitude), and
is the Latitude), and ![]() to
be distance (Radius) from a point to the Origin.
to
be distance (Radius) from a point to the Origin.
Unfortunately, the convention in which the symbols ![]() and
and ![]() are reversed is frequently used, especially in physics,
leading to unnecessary confusion. The symbol
are reversed is frequently used, especially in physics,
leading to unnecessary confusion. The symbol ![]() is sometimes also used in place of
is sometimes also used in place of ![]() . Arfken (1985) uses
. Arfken (1985) uses
![]() , whereas Beyer (1987) uses
, whereas Beyer (1987) uses
![]() . Be very careful when consulting the literature.
. Be very careful when consulting the literature.
In this work, the symbols for the azimuthal, polar, and radial coordinates are taken as ![]() ,
, ![]() , and
, and ![]() ,
respectively. Note that this definition provides a logical extension of the usual Polar Coordinates notation, with
,
respectively. Note that this definition provides a logical extension of the usual Polar Coordinates notation, with
![]() remaining the Angle in the
remaining the Angle in the ![]() -Plane and
-Plane and ![]() becoming the Angle out of the Plane.
becoming the Angle out of the Plane.
| (1) | |||
| (2) | |||
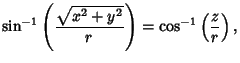 |
(3) |
| (4) | |||
| (5) | |||
| (6) |
| (7) | |||
| (8) | |||
| (9) |
| (10) | |||
| (11) | |||
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
The Position Vector is
![\begin{displaymath}
{\bf r} \equiv\left[{\matrix{r\cos\theta\sin\phi\cr r\sin\theta\sin\phi\cr r\cos\phi\cr}}\right],
\end{displaymath}](s2_942.gif) |
(17) |
![$\displaystyle {{d{\bf r}\over dr}\over \left\vert{d{\bf r}\over dr}\right\vert}...
...array}{c}\cos\theta\sin\phi\\ \sin\theta\sin\phi\\ \cos\phi\end{array}\right]$](s2_944.gif) |
(18) | ||
![$\displaystyle {{d{\bf r}\over d\theta}\over \left\vert{d{\bf r}\over d\theta}\r...
...\vert} = \left[\begin{array}{c}-\sin\theta\\ \cos\theta\\ 0\end{array}\right]$](s2_946.gif) |
(19) | ||
![$\displaystyle {{d{\bf r}\over d\phi}\over \left\vert{d{\bf r}\over d\phi }\righ...
...ray}{c}\cos\theta\cos\phi\\ \sin\theta\cos\phi\\ -\sin\phi\end{array}\right].$](s2_948.gif) |
(20) |
Derivatives of the Unit Vectors are
| (21) | |||
| (22) | |||
| (23) | |||
![$\displaystyle \left[\begin{array}{c}-\sin\theta\sin\phi\\ \cos\theta\sin\phi\\ 0\end{array}\right] =\sin\phi\,\hat{\boldsymbol{\theta}}$](s2_954.gif) |
(24) | ||
![$\displaystyle \left[\begin{array}{c}-\cos\theta\\ -\sin\theta\\ 0\end{array}\right]=-\cos\phi\,\hat{\boldsymbol{\phi}}-\sin\phi\,\hat{\bf r}$](s2_956.gif) |
(25) | ||
![$\displaystyle \left[\begin{array}{c}-\sin\theta\cos\phi\\ \cos\theta\cos\phi\\ 0\end{array}\right]=\cos\phi\,\hat{\boldsymbol{\theta}}$](s2_958.gif) |
(26) | ||
![$\displaystyle \left[\begin{array}{c}\cos\theta\\ \sin\theta\cos\phi\\ -\sin\phi\end{array}\right] =\hat {\boldsymbol{\phi}}$](s2_960.gif) |
(27) | ||
| (28) | |||
![$\displaystyle \left[\begin{array}{c}-\cos\theta\sin\phi\\ -\sin\theta\sin\phi\\ -\cos\phi\end{array}\right]=- \hat {\bf r}.$](s2_963.gif) |
(29) |
The Gradient is
| (30) |
| (31) | |||
| (32) | |||
| (33) | |||
 |
(34) | ||
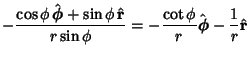 |
(35) | ||
 |
(36) |
Now, since the Connection Coefficients are given by
![]() ,
,
![$\displaystyle \left[\begin{array}{ccc}0 & {1\over r} & 0\\ 0 & 0 & 0\\ 0 & {\cot\phi\over r} & 0\end{array}\right]$](s2_977.gif) |
(37) | ||
![$\displaystyle \left[\begin{array}{ccc}0 & 0 & {1\over r}\\ 0 & -{\cot\phi\over r} & 0\\ 0 & 0 & 0\end{array}\right]$](s2_979.gif) |
(38) | ||
![$\displaystyle \left[\begin{array}{ccc}0 & 0 & 0\\ 0 & -{1\over r} & 0\\ 0 & 0 & -{1\over r}\end{array}\right].$](s2_981.gif) |
(39) |
The Divergence is
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(40) |
 |
|||
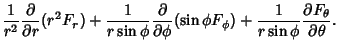 |
(41) |
The Covariant Derivatives are given by
| (42) |
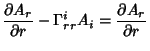 |
(43) | ||
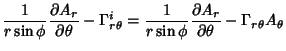 |
|||
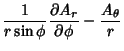 |
(44) | ||
 |
|||
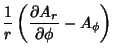 |
(45) | ||
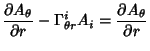 |
(46) | ||
 |
|||
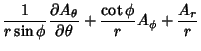 |
(47) | ||
 |
(48) | ||
 |
(49) | ||
 |
|||
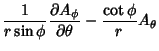 |
(50) | ||
 |
|||
 |
(51) |
The Commutation Coefficients are given by
| (52) |
| (53) |
| (54) |
| (55) |
| (56) |
| (57) |
![$\displaystyle \left[\begin{array}{ccc}0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right]$](s2_1029.gif) |
(58) | ||
![$\displaystyle \left[\begin{array}{ccc}0 & -{1\over r} & 0\\ {1\over r} & 0 &{1\over r}\cot\phi\\ 0 & -{1\over r}\cot\phi & 0\end{array}\right]$](s2_1031.gif) |
(59) | ||
![$\displaystyle \left[\begin{array}{ccc}0 & 0 & -{1\over r}\\ 0 & 0 & 0\\ {1\over r} & 0 & 0\end{array}\right].$](s2_1033.gif) |
(60) |
Time derivatives of the Position Vector are
![$\displaystyle \left[\begin{array}{c}\cos\theta\sin\phi\,\dot r-r\sin\theta\sin\...
...eta\cos\phi\,\dot\phi\\ \cos\phi\,\dot r-r\sin\phi\,\dot\phi\end{array}\right]$](s2_1035.gif) |
|||
![$\displaystyle \left[\begin{array}{c}\cos\theta\sin\phi\\ \sin\theta\sin\phi\\ ...
...\cos\theta\cos\phi\\ \sin\theta\cos\phi\\ -\sin\phi\end{array}\right]\dot\phi$](s2_1036.gif) |
|||
| (61) |
| (62) |
| (63) | |||
| (64) | |||
| (65) |
![$\displaystyle (\ddot r-r\dot\phi^2)\left[\begin{array}{c}\cos\theta\sin\phi\\ \sin\theta\sin\phi\\ \cos\phi\end{array}\right]$](s2_1059.gif) |
|||
![$\displaystyle +(2r\cos\phi\dot\theta\dot\phi +r\sin\phi\ddot\theta)\left[\begin{array}{c}-\sin\theta\\ \cos\theta\\ 0\end{array}\right]$](s2_1060.gif) |
|||
![$\displaystyle \mathop{+}(2\dot r\dot\phi +r\ddot\phi)\left[\begin{array}{c}\cos...
...\left[\begin{array}{c}\cos\theta\\ \sin\theta\\ 0\end{array}\right],\nonumber$](s2_1061.gif) |
|||
| (66) |
![$\displaystyle \left[\begin{array}{c}\cos\theta\sin^2\phi
+\cos\theta\cos^2\phi\\ \sin\theta\sin^2\phi +\sin\theta\cos^2\phi\\ 0\end{array}\right]$](s2_1063.gif) |
|||
![$\displaystyle \left[\begin{array}{c}\cos\theta\\ \sin\theta\\ 0\end{array}\right],$](s2_1064.gif) |
(67) |
| (68) |
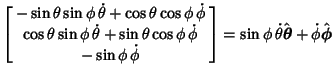 |
|||
| (69) | |||
![$\displaystyle \left[\begin{array}{c}-\cos\theta\dot\theta\\ -\sin\theta\dot\th...
...nd{array}\right]=-\dot\theta(\sin\phi\hat{\bf r}+\cos\phi\hat\boldsymbol{\phi})$](s2_1073.gif) |
|||
| (70) | |||
![$\displaystyle \left[\begin{array}{c}-\sin\theta\cos\phi\,\dot\theta-\cos\theta\...
...}\right] = -\dot\phi\hat {\bf r} +\cos\phi\dot\theta\hat {\boldsymbol{\theta}}.$](s2_1075.gif) |
|||
| (71) |
The Curl is
|
|
|
|
|
|
|
|
(72) |
The Laplacian is
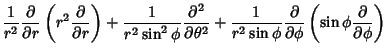 |
|||
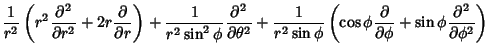 |
|||
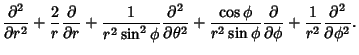 |
(73) |
![\begin{displaymath}
\nabla^2 {\bf v}=\left[\begin{array}{l}
{1\over r}{\partial^...
...al\phi} -{v_\phi\over r^2\sin^2\theta}}\\
\end{array}\right].
\end{displaymath}](s2_1082.gif) |
(74) |
To express Partial Derivatives with respect to Cartesian axes in terms of Partial Derivatives of the spherical coordinates,
![$\displaystyle \left[\begin{array}{c}r\cos\theta\sin\phi\\ r\sin\theta\sin\phi\\ r\cos\phi\end{array}\right]$](s2_1084.gif) |
(75) | ||
![$\displaystyle \left[\begin{array}{c}\cos\theta\sin\phi\,dr-r\sin\theta\sin\phi\...
...a+r\sin\theta\cos\phi\,d\phi\\ \cos\phi\,dr-r\sin\phi\,d\phi\end{array}\right]$](s2_1086.gif) |
|||
![$\displaystyle \left[\begin{array}{ccc}\cos\theta\sin\phi & -r\sin\theta\sin\phi...
...nd{array}\right]\left[\begin{array}{c}dr\\ d\theta\\ d\phi\end{array}\right].$](s2_1087.gif) |
|||
| (76) |
Upon inversion, the result is
![\begin{displaymath}
\left[{\matrix{dr\cr d\theta\cr d\phi\cr}}\right]
=\left[{\...
...trix{dx\cr dy\cr dz\cr}}\right].
\hrule width 0pt height 6.1pt
\end{displaymath}](s2_1088.gif) |
(77) |
 |
|||
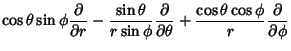 |
|||
| (78) | |||
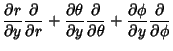 |
|||
 |
|||
| (79) | |||
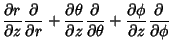 |
|||
 |
(80) |
The Helmholtz Differential Equation is separable in spherical coordinates.
See also Colatitude, Great Circle, Helmholtz Differential Equation--Spherical Coordinates, Latitude, Longitude, Oblate Spheroidal Coordinates, Prolate Spheroidal Coordinates
References
Arfken, G. ``Spherical Polar Coordinates.'' §2.5 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 102-111, 1985.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 212, 1987.
Gasiorowicz, S. Quantum Physics. New York: Wiley, 1974.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 658, 1953.
|
|
|
© 1996-9 Eric W. Weisstein