|
|
|
Let a particle travel a distance ![]() as a function of time
as a function of time ![]() (here,
(here, ![]() can be thought of as the Arc
Length of the curve traced out by the particle). The Speed (the Scalar Norm of the
Vector Velocity) is then given by
can be thought of as the Arc
Length of the curve traced out by the particle). The Speed (the Scalar Norm of the
Vector Velocity) is then given by
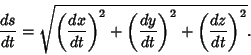 |
(1) |
| (2) | |||
| (3) | |||
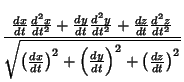 |
(4) | ||
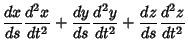 |
(5) | ||
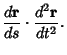 |
(6) |
| (7) |
Let a particle move along a straight Line so that the positions at times ![]() ,
, ![]() , and
, and ![]() are
are ![]() ,
, ![]() ,
and
,
and ![]() , respectively. Then the particle is uniformly accelerated with acceleration
, respectively. Then the particle is uniformly accelerated with acceleration ![]() Iff
Iff
| (8) |
Consider the measurement of acceleration in a rotating reference frame. Apply the Rotation Operator
| (9) |
 |
|||
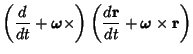 |
|||
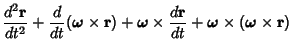 |
|||
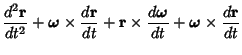 |
|||
| (10) |
| (11) |
| (12) | |||
| (13) | |||
| (14) |
| (15) |
See also Angular Acceleration, Arc Length, Jerk, Velocity
References
Klamkin, M. S. ``Problem 1481.'' Math. Mag. 68, 307, 1995.
Klamkin, M. S. ``A Characteristic of Constant Acceleration.'' Solution to Problem 1481. Math. Mag. 69, 308, 1996.
|
|
|
© 1996-9 Eric W. Weisstein