|
|
|
For a curve with Position Vector ![]() , the unit tangent vector
, the unit tangent vector
![]() is defined by
is defined by
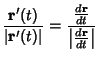 |
(1) | ||
| (2) | |||
| (3) |
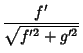 |
(4) | ||
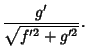 |
(5) |
| (6) | |||
| (7) | |||
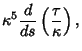 |
(8) |
See also Curvature, Normal Vector, Tangent, Tangent Bundle, Tangent Plane, Tangent Space, Torsion (Differential Geometry)
References
Gray, A. ``Tangent and Normal Lines to Plane Curves.'' §5.5 in
Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 85-90, 1993.