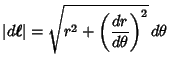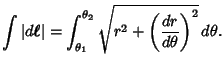Arc length is defined as the length along a curve,
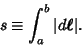 |
(1) |
Defining the line element
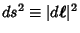 , parameterizing the curve in terms of a parameter
, parameterizing the curve in terms of a parameter  , and noting
that
, and noting
that 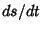 is simply the magnitude of the Velocity with which the end of the Radius Vector
is simply the magnitude of the Velocity with which the end of the Radius Vector 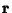 moves gives
moves gives
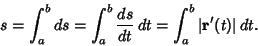 |
(2) |
In Polar Coordinates,
 |
(3) |
so
In Cartesian Coordinates,
Therefore, if the curve is written
 |
(8) |
then
 |
(9) |
If the curve is instead written
 |
(10) |
then
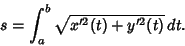 |
(11) |
Or, in three dimensions,
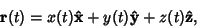 |
(12) |
so
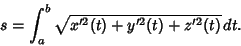 |
(13) |
See also Curvature, Geodesic, Normal Vector, Radius of Curvature, Radius of Torsion,
Speed, Surface Area, Tangential Angle, Tangent Vector, Torsion (Differential Geometry),
Velocity
© 1996-9 Eric W. Weisstein
1999-05-25