Given two points on a surface, the geodesic is defined as the shortest path on the surface connecting them. Geodesics
have many interesting properties. The Normal Vector to any point of a Geodesic arc lies along the normal
to a surface at that point (Weinstock 1974, p. 65).
Furthermore, no matter how badly a Sphere is distorted, there exist an infinite number of closed
geodesics on it. This general result, demonstrated in the early 1990s, extended earlier work by Birkhoff, who proved in 1917
that there exists at least one closed geodesic on a distorted sphere, and Lyusternik and Schnirelmann, who proved in 1923 that there
exist at least three closed geodesics on such a sphere (Cipra 1993).
For a surface given parametrically by 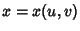 ,
, 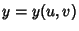 , and
, and 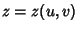 , the geodesic can be found by minimizing the
Arc Length
, the geodesic can be found by minimizing the
Arc Length
 |
(1) |
But
and similarly for  and
and  . Plugging in,
. Plugging in,
This can be rewritten as
where
and
Taking derivatives,
so the Euler-Lagrange Differential Equation then gives
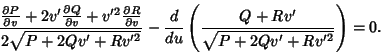 |
(14) |
In the special case when 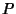 ,
, 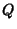 , and
, and 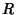 are explicit functions of
are explicit functions of 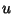 only,
only,
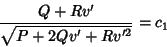 |
(15) |
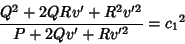 |
(16) |
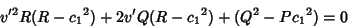 |
(17) |
![\begin{displaymath}
v'={1\over 2R(R-{c_1}^2)}[2Q({c_1}^2-R)\pm\sqrt{4Q^2(R-{c_1}^2)^2-4R(R-{c_1}^2)(Q^2-P{c_1}^2)}\,].
\end{displaymath}](g_1286.gif) |
(18) |
Now, if 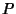 and
and 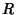 are explicit functions of
are explicit functions of 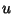 only and
only and  ,
,
 |
(19) |
so
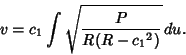 |
(20) |
In the case  where
where 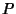 and
and 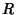 are explicit functions of
are explicit functions of 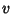 only, then
only, then
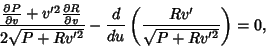 |
(21) |
so
![\begin{displaymath}
{\partial P\over \partial v}+v'^2{\partial R\over\partial v}...
...style{1\over 2}}) {v'(2Rv'v'')\over (P+Rv'^2)^{3/2}}}\right]=0
\end{displaymath}](g_1291.gif) |
(22) |
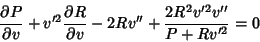 |
(23) |
 |
(24) |
 |
(25) |
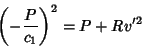 |
(26) |
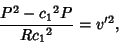 |
(27) |
and
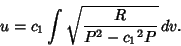 |
(28) |
For a Surface of Revolution in which 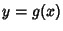 is rotated about the
is rotated about the  -axis so that the equation of the surface is
-axis so that the equation of the surface is
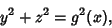 |
(29) |
the surface can be parameterized by
The equation of the geodesics is then
![\begin{displaymath}
v=c_1 \int {\sqrt{1+[g'(u)]^2}\,du\over g(u)\sqrt{[g(u)]^2-{c_1}^2}}.
\end{displaymath}](g_1303.gif) |
(33) |
See also Ellipsoid Geodesic, Geodesic Curvature, Geodesic Dome, Geodesic Equation, Geodesic
Triangle, Great Circle, Harmonic Map, Oblate Spheroid Geodesic, Paraboloid Geodesic
References
Cipra, B. What's Happening in the Mathematical Sciences, Vol. 1.
Providence, RI: Amer. Math. Soc., pp. 27, 1993.
Weinstock, R. Calculus of Variations, with Applications to Physics and Engineering. New York: Dover,
pp. 26-28 and 45-46, 1974.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ,
, ![]() , and
, and ![]() , the geodesic can be found by minimizing the
Arc Length
, the geodesic can be found by minimizing the
Arc Length
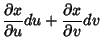
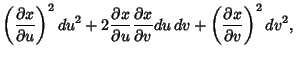
![$\displaystyle \int\left\{{\left[{\left({\partial x\over \partial u}\right)^2+\l...
...al u}\right)^2
+\left({\partial z\over \partial u}\right)^2}\right]du^2}\right.$](g_1262.gif)
![$\displaystyle \mathop{+} 2\left[{{\partial x\over \partial u}{\partial x\over\p...
... v}
+{\partial z\over \partial u}{\partial z\over \partial v}}\right]\, du\, dv$](g_1263.gif)
![$\displaystyle \mathop{+}\left.{\left[{\left({\partial x\over \partial v}\right)...
...)^2
+\left({\partial z\over \partial v}\right)^2}\right]\, dv^2}\right\}^{1/2}.$](g_1264.gif)
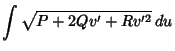
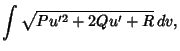

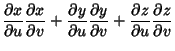
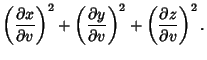
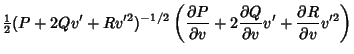
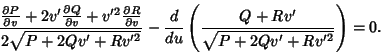
![]() ,
, ![]() , and
, and ![]() are explicit functions of
are explicit functions of ![]() only,
only,
![]() and
and ![]() are explicit functions of
are explicit functions of ![]() only and
only and ![]() ,
,

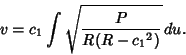
![\begin{displaymath}
v=c_1 \int {\sqrt{1+[g'(u)]^2}\,du\over g(u)\sqrt{[g(u)]^2-{c_1}^2}}.
\end{displaymath}](g_1303.gif)