An Ellipsoid can be specified parametrically by
The Geodesic parameters are then
When the coordinates of a point are on the Quadric
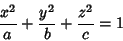 |
(7) |
and expressed in terms of the parameters 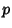 and
and 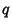 of the confocal quadrics passing through that point (in other words,
having
of the confocal quadrics passing through that point (in other words,
having 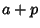 ,
, 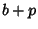 ,
, 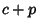 , and
, and 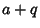 ,
,  ,
,  for the squares of their semimajor axes), then the equation of a
Geodesic can be expressed in the form
for the squares of their semimajor axes), then the equation of a
Geodesic can be expressed in the form
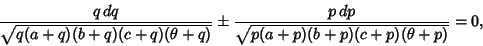 |
(8) |
with 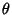 an arbitrary constant, and the Arc Length element
an arbitrary constant, and the Arc Length element  is given by
is given by
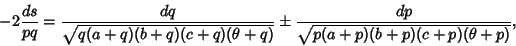 |
(9) |
where upper and lower signs are taken together.
See also Oblate Spheroid Geodesic, Sphere Geodesic
References
Eisenhart, L. P. A Treatise on the Differential Geometry of Curves and Surfaces. New York: Dover, pp. 236-241, 1960.
Forsyth, A. R. Calculus of Variations. New York: Dover, p. 447, 1960.
© 1996-9 Eric W. Weisstein
1999-05-25