A sphere is defined as the set of all points in 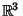 which are a distance
which are a distance  (the ``Radius'') from a given
point (the ``Center''). Twice the Radius is called the Diameter, and pairs of points on opposite sides
of a Diameter are called Antipodes. The term ``sphere'' technically refers to the outer surface of
a ``Bubble,'' which is denoted
(the ``Radius'') from a given
point (the ``Center''). Twice the Radius is called the Diameter, and pairs of points on opposite sides
of a Diameter are called Antipodes. The term ``sphere'' technically refers to the outer surface of
a ``Bubble,'' which is denoted 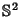 . However, in common usage, the word sphere is also used to mean the
Union of a sphere and its Interior (a ``solid sphere''), where the Interior is called a Ball. The
Surface Area of the sphere and Volume of the Ball of Radius
. However, in common usage, the word sphere is also used to mean the
Union of a sphere and its Interior (a ``solid sphere''), where the Interior is called a Ball. The
Surface Area of the sphere and Volume of the Ball of Radius  are given by
are given by
(Beyer 1987, p. 130). In On the Sphere and Cylinder (ca. 225 BC  ), Archimedes
), Archimedes  became the first to
derive these equations (although he expressed
became the first to
derive these equations (although he expressed 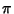 in terms of the sphere's circular cross-section). The fact that
in terms of the sphere's circular cross-section). The fact that
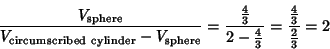 |
(3) |
was also known to Archimedes. 
Any cross-section through a sphere is a Circle (or, in the degenerate case where the slicing Plane is tangent to
the sphere, a point). The size of the Circle is maximized when the Plane defining the cross-section passes
through a Diameter.
The equation of a sphere of Radius  is given in Cartesian Coordinates by
is given in Cartesian Coordinates by
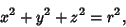 |
(4) |
which is a special case of the Ellipsoid
 |
(5) |
and Spheroid
 |
(6) |
A sphere may also be specified in Spherical Coordinates by
where  is an azimuthal coordinate running from 0 to
is an azimuthal coordinate running from 0 to  (Longitude),
(Longitude), 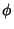 is a polar coordinate running
from 0 to
is a polar coordinate running
from 0 to 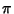 (Colatitude), and
(Colatitude), and  is the Radius. Note that there are several other notations
sometimes used in which the symbols for
is the Radius. Note that there are several other notations
sometimes used in which the symbols for  and
and 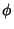 are interchanged or where
are interchanged or where  is used instead of
is used instead of  . If
. If
 is allowed to run from 0 to a given Radius
is allowed to run from 0 to a given Radius  , then a solid Ball is obtained.
Converting to ``standard'' parametric variables
, then a solid Ball is obtained.
Converting to ``standard'' parametric variables 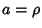 ,
,  , and
, and 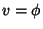 gives the first Fundamental
Forms
gives the first Fundamental
Forms
second Fundamental Forms
Area Element
 |
(16) |
Gaussian Curvature
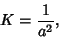 |
(17) |
and Mean Curvature
 |
(18) |
A sphere may also be represented parametrically by letting
 , so
, so
where  runs from 0 to
runs from 0 to  and
and 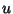 runs from
runs from 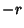 to
to  .
.
Given two points on a sphere, the shortest path on the surface of the sphere which connects them (the Sphere Geodesic)
is an Arc of a Circle known as a Great Circle. The equation of the sphere with points
 and
and
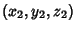 lying on a Diameter is given by
lying on a Diameter is given by
 |
(22) |
Four points are sufficient to uniquely define a sphere. Given the points
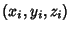 with
with 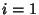 , 2, 3, and 4, the
sphere containing them is given by the beautiful Determinant equation
, 2, 3, and 4, the
sphere containing them is given by the beautiful Determinant equation
 |
(23) |
(Beyer 1987, p. 210).
The generalization of a sphere in 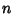 dimensions is called a Hypersphere. An
dimensions is called a Hypersphere. An 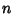 -D Hypersphere can
be specified by the equation
-D Hypersphere can
be specified by the equation
 |
(24) |
The distribution of Angles for random rotation of a sphere is
 |
(25) |
giving a Mean of  .
.
To pick a random point on the surface of a sphere, let 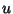 and
and  be random variates on
be random variates on ![$[0,1]$](s2_723.gif) . Then
. Then
This works since the Solid Angle is
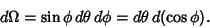 |
(28) |
Another easy way to pick a random point on a Sphere is to generate three gaussian random variables 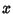 ,
, 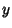 , and
, and 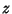 .
Then the distribution of the vectors
.
Then the distribution of the vectors
![\begin{displaymath}
{1\over\sqrt{x^2+y^2+z^2}}\left[{\matrix{x\cr y\cr z\cr}}\right]
\end{displaymath}](s2_729.gif) |
(29) |
is uniform over the surface 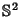 . Another method is to pick
. Another method is to pick 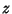 from a Uniform Distribution over
from a Uniform Distribution over ![$[-1,1]$](s2_730.gif) and
and
 from a Uniform Distribution over
from a Uniform Distribution over 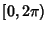 . Then the points
. Then the points
![\begin{displaymath}
\left[{\matrix{\sqrt{1-z^2}\cos\theta\cr \sqrt{1-z^2}\sin\theta\cr z\cr}}\right]
\end{displaymath}](s2_732.gif) |
(30) |
are uniformly distributed over 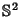 .
.
Pick four points on a sphere. What is the probability that the Tetrahedron having these points as
Vertices contains the Center of the sphere? In the 1-D case, the probability that a
second point is on the opposite side of 1/2 is 1/2. In the 2-D case, pick two points. In order for the third to form a
Triangle containing the Center, it must lie in the quadrant bisected by a Line Segment passing through
the center of the Circle and the bisector of the two points. This happens for one Quadrant, so the probability
is 1/4. Similarly, for a sphere the probability is one Octant, or 1/8.
Pick two points at random on a unit sphere. The first one can be assigned the coordinate (0, 0, 1) without loss of
generality. The second point can be given the coordinates
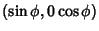 with
with
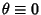 since all points
with the same
since all points
with the same 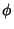 are rotationally identical. The distance between the two points is then
are rotationally identical. The distance between the two points is then
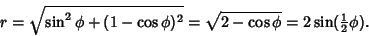 |
(31) |
Because the surface Area element is
 |
(32) |
the probability that two points are a distance  apart is
apart is
The Delta Function contributes when
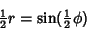 |
(34) |
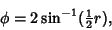 |
(35) |
so
However, we need
 |
(37) |
and
so
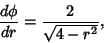 |
(39) |
and
 |
(40) |
for ![$r\in[0,2]$](s2_750.gif) . Somewhat surprisingly, the largest distances are the most common, contrary to most people's intuition. A
plot of 15 random lines is shown below.
. Somewhat surprisingly, the largest distances are the most common, contrary to most people's intuition. A
plot of 15 random lines is shown below.
The Moments about zero are
 |
(41) |
giving the first few as
Moments about the Mean are
so the Skewness and Kurtosis are
See also Ball, Bing's Theorem, Bubble, Circle, Dandelin Spheres, Diameter,
Ellipsoid, Exotic Sphere, Fejes Tóth's Problem, Hypersphere,
Liebmann's Theorem, Liouville's Sphere-Preserving Theorem, Mikusinski's Problem, Noise Sphere, Oblate Spheroid, Osculating Sphere, Parallelizable, Prolate
Spheroid, Radius, Space Division, Sphere Packing, Tennis Ball Theorem
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press,
1987.
Eppstein, D. ``Circles and Spheres.''
http://www.ics.uci.edu/~eppstein/junkyard/sphere.html.
Geometry Center. ``The Sphere.'' http://www.geom.umn.edu/zoo/toptype/sphere/.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() which are a distance
which are a distance ![]() (the ``Radius'') from a given
point (the ``Center''). Twice the Radius is called the Diameter, and pairs of points on opposite sides
of a Diameter are called Antipodes. The term ``sphere'' technically refers to the outer surface of
a ``Bubble,'' which is denoted
(the ``Radius'') from a given
point (the ``Center''). Twice the Radius is called the Diameter, and pairs of points on opposite sides
of a Diameter are called Antipodes. The term ``sphere'' technically refers to the outer surface of
a ``Bubble,'' which is denoted ![]() . However, in common usage, the word sphere is also used to mean the
Union of a sphere and its Interior (a ``solid sphere''), where the Interior is called a Ball. The
Surface Area of the sphere and Volume of the Ball of Radius
. However, in common usage, the word sphere is also used to mean the
Union of a sphere and its Interior (a ``solid sphere''), where the Interior is called a Ball. The
Surface Area of the sphere and Volume of the Ball of Radius ![]() are given by
are given by
![]() is given in Cartesian Coordinates by
is given in Cartesian Coordinates by
![]() and
and
![]() lying on a Diameter is given by
lying on a Diameter is given by
![]() with
with ![]() , 2, 3, and 4, the
sphere containing them is given by the beautiful Determinant equation
, 2, 3, and 4, the
sphere containing them is given by the beautiful Determinant equation

![]() dimensions is called a Hypersphere. An
dimensions is called a Hypersphere. An ![]() -D Hypersphere can
be specified by the equation
-D Hypersphere can
be specified by the equation
![]() and
and ![]() be random variates on
be random variates on ![]() . Then
. Then
![\begin{displaymath}
{1\over\sqrt{x^2+y^2+z^2}}\left[{\matrix{x\cr y\cr z\cr}}\right]
\end{displaymath}](s2_729.gif)
![\begin{displaymath}
\left[{\matrix{\sqrt{1-z^2}\cos\theta\cr \sqrt{1-z^2}\sin\theta\cr z\cr}}\right]
\end{displaymath}](s2_732.gif)
![]() with
with
![]() since all points
with the same
since all points
with the same ![]() are rotationally identical. The distance between the two points is then
are rotationally identical. The distance between the two points is then
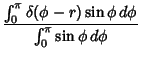
![$\displaystyle {\textstyle{1\over 2}}\int_0^\pi \delta[r-2\sin({\textstyle{1\over 2}}\phi)]\sin\phi\,d\phi.$](s2_739.gif)