|
|
|
There are three types of so-called fundamental forms. The most important are the first and second (since the third
can be expressed in terms of these). The fundamental forms are extremely important and useful in determining the
metric properties of a surface, such as Line Element, Area Element, Normal Curvature,
Gaussian Curvature, and Mean Curvature. Let ![]() be a Regular Surface with
be a Regular Surface with
![]() points on the Tangent Space
points on the Tangent Space ![]() of
of ![]() . Then the first fundamental form is the
Inner Product of tangent vectors,
. Then the first fundamental form is the
Inner Product of tangent vectors,
| (1) |
| (2) |
| (3) |
The first and second fundamental forms satisfy
| (4) | |||
| (5) |
| (6) |
| (7) |
The first fundamental form (or Line Element) is given explicitly by the Riemannian Metric
| (8) |
 |
(9) | ||
 |
(10) | ||
 |
(11) |
| (12) | |||
| (13) |
The second fundamental form is given explicitly by
| (14) |
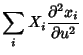 |
(15) | ||
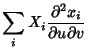 |
(16) | ||
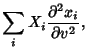 |
(17) |
| (18) | |||
| (19) | |||
| (20) |
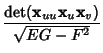 |
(21) | ||
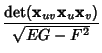 |
(22) | ||
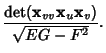 |
(23) |
See also Arc Length, Area Element, Gaussian Curvature, Geodesic, Kähler Manifold, Line of Curvature, Line Element, Mean Curvature, Normal Curvature, Riemannian Metric, Scale Factor, Weingarten Equations
References
Gray, A. ``The Three Fundamental Forms.'' §14.6 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 251-255, 259-260, 275-276, and 282-291, 1993.
|
|
|
© 1996-9 Eric W. Weisstein