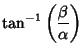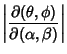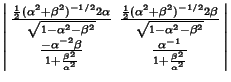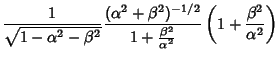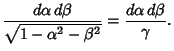Let 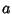 be the Angle between
be the Angle between 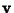 and
and 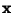 ,
, 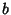 the Angle between
the Angle between 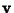 and
and 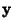 , and
, and 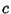 the Angle between
the Angle between 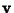 and
and 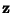 . Then the direction cosines are equivalent to the
. Then the direction cosines are equivalent to the 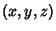 coordinates
of a Unit Vector
coordinates
of a Unit Vector 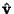 ,
,
 |
(1) |
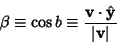 |
(2) |
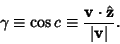 |
(3) |
From these definitions, it follows that
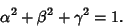 |
(4) |
To find the Jacobian when performing integrals over direction cosines, use
The Jacobian is
 |
(8) |
Using
so
Direction cosines can also be defined between two sets of Cartesian Coordinates,
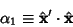 |
(13) |
 |
(14) |
 |
(15) |
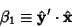 |
(16) |
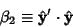 |
(17) |
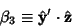 |
(18) |
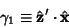 |
(19) |
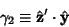 |
(20) |
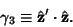 |
(21) |
Projections of the unprimed coordinates onto the primed coordinates yield
and
Projections of the primed coordinates onto the unprimed coordinates yield
and
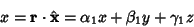 |
(31) |
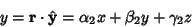 |
(32) |
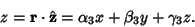 |
(33) |
Using the orthogonality of the coordinate system, it must be true that
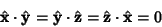 |
(34) |
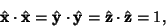 |
(35) |
giving the identities
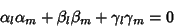 |
(36) |
for
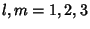 and
and 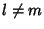 , and
, and
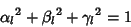 |
(37) |
for 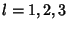 . These two identities may be combined into the single identity
. These two identities may be combined into the single identity
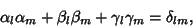 |
(38) |
where 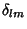 is the Kronecker Delta.
is the Kronecker Delta.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() be the Angle between
be the Angle between ![]() and
and ![]() ,
, ![]() the Angle between
the Angle between ![]() and
and ![]() , and
, and ![]() the Angle between
the Angle between ![]() and
and ![]() . Then the direction cosines are equivalent to the
. Then the direction cosines are equivalent to the ![]() coordinates
of a Unit Vector
coordinates
of a Unit Vector ![]() ,
,