|
|
|
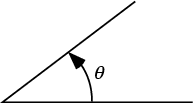
Given two intersecting Lines or Line Segments, the amount of Rotation about
the point of intersection (the Vertex) required to bring one into correspondence with the other is called the angle
![]() between them. Angles are usually measured in Degrees (denoted °),
Radians (denoted rad, or without a unit), or sometimes Gradians (denoted grad).
between them. Angles are usually measured in Degrees (denoted °),
Radians (denoted rad, or without a unit), or sometimes Gradians (denoted grad).
One full rotation in these three measures corresponds to 360°, ![]() rad, or 400 grad. Half a full
Rotation is called a Straight Angle, and a Quarter of a full rotation is called a Right Angle.
An angle less than a Right Angle is called an Acute Angle, and an angle greater than a Right Angle is
called an Obtuse Angle.
rad, or 400 grad. Half a full
Rotation is called a Straight Angle, and a Quarter of a full rotation is called a Right Angle.
An angle less than a Right Angle is called an Acute Angle, and an angle greater than a Right Angle is
called an Obtuse Angle.
The use of Degrees to measure angles harks back to the Babylonians, whose Sexagesimal number
system was based on the number 60. 360° likely arises from the Babylonian year, ![]() which was composed of
360 days (12 months
which was composed of
360 days (12 months ![]() of 30 days
of 30 days ![]() each). The Degree is further divided into
60 Arc Minutes, and an Arc Minute into 60 Arc Seconds. A more natural
measure of an angle is the Radian. It has the property that the Arc Length around a Circle is simply
given by the radian angle measure times the Circle Radius. The Radian is also the most useful angle
measure in Calculus because the Derivative of Trigonometric functions such as
each). The Degree is further divided into
60 Arc Minutes, and an Arc Minute into 60 Arc Seconds. A more natural
measure of an angle is the Radian. It has the property that the Arc Length around a Circle is simply
given by the radian angle measure times the Circle Radius. The Radian is also the most useful angle
measure in Calculus because the Derivative of Trigonometric functions such as
The concept of an angle can be generalized from the Circle to the Sphere. The fraction of a Sphere
subtended by an object is measured in Steradians, with the entire Sphere corresponding
to ![]() Steradians.
Steradians.
A ruled Semicircle used for measuring and drawing angles is called a Protractor. A Compass can also be used to draw circular Arcs of some angular extent.
See also Acute Angle, Arc Minute, Arc Second, Central Angle, Complementary Angle, Degree, Dihedral Angle, Directed Angle, Euler Angles, Gradian, Horn Angle, Inscribed Angle, Oblique Angle, Obtuse Angle, Perigon, Protractor, Radian, Right Angle, Solid Angle, Steradian, Straight Angle, Subtend, Supplementary Angle, Vertex Angle
References
Dixon, R. Mathographics. New York: Dover, pp. 99-100, 1991.
|
|
|
© 1996-9 Eric W. Weisstein