|
|
|
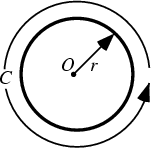
A circle is the set of points equidistant from a given point ![]() . The distance
. The distance ![]() from the Center is called the
Radius, and the point
from the Center is called the
Radius, and the point ![]() is called the Center. Twice the Radius is known as the Diameter
is called the Center. Twice the Radius is known as the Diameter
![]() . The Perimeter
. The Perimeter ![]() of a circle is called the Circumference, and is given by
of a circle is called the Circumference, and is given by
| (1) |
The region of intersection of two circles is called a Lens. The region of intersection of three symmetrically placed circles (as in a Venn Diagram), in the special case of the center of each being located at the intersection of the other two, is called a Reuleaux Triangle.
The parametric equations for a circle of Radius ![]() are
are
| (2) | |||
| (3) |
| (4) | |||
| (5) |
| (6) | |||
| (7) |
| (8) | |||
| (9) |

The Arc Length ![]() , Curvature
, Curvature ![]() , and Tangential Angle
, and Tangential Angle ![]() of the circle are
of the circle are
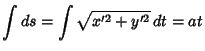 |
(10) | ||
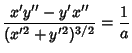 |
(11) | ||
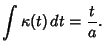 |
(12) |
| (13) |
In Polar Coordinates, the equation of the circle has a particularly simple form.
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
The equation of a circle passing through the three points ![]() for
for ![]() , 2, 3 (the Circumcircle of the
Triangle determined by the points) is
, 2, 3 (the Circumcircle of the
Triangle determined by the points) is
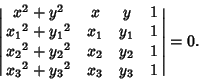 |
(20) |
| (21) |
| (22) |
| (23) | |||
| (24) |
| (25) |
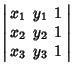 |
(26) | ||
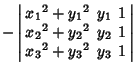 |
(27) | ||
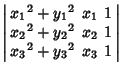 |
(28) | ||
 |
(29) |
The Circumference-to-Diameter ratio ![]() for a circle is constant as the size of the circle is changed (as
it must be since scaling a plane figure by a factor
for a circle is constant as the size of the circle is changed (as
it must be since scaling a plane figure by a factor ![]() increases its Perimeter by
increases its Perimeter by ![]() ), and
), and ![]() also scales by
also scales by
![]() . This ratio is denoted
. This ratio is denoted ![]() (Pi), and has been proved Transcendental.
With
(Pi), and has been proved Transcendental.
With ![]() the Diameter and
the Diameter and ![]() the Radius,
the Radius,
| (30) |
| (31) |
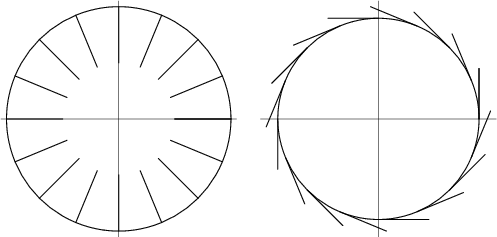
Now for a few geometrical derivations. Using concentric strips, we have
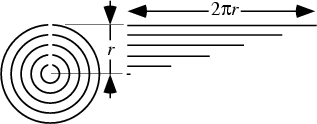
As the number of strips increases to infinity, we are left with a Triangle on the right, so
| (32) |
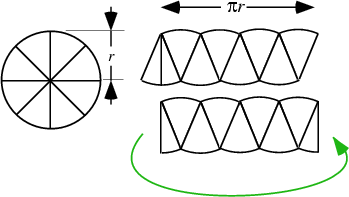
As the number of wedges increases to infinity, we are left with a Rectangle, so
| (33) |
See also Arc, Blaschke's Theorem, Brahmagupta's Formula, Brocard Circle, Casey's Theorem, Chord, Circumcircle, Circumference, Clifford's Circle Theorem, Closed Disk, Concentric Circles, Cosine Circle, Cotes Circle Property, Diameter, Disk, Droz-Farny Circles, Euler Triangle Formula, Excircle, Feuerbach's Theorem, Five Disks Problem, Flower of Life, Ford Circle, Fuhrmann Circle, Gersgorin Circle Theorem, Hopf Circle, Incircle, Inversive Distance, Johnson Circle, Kinney's Set, Lemoine Circle, Lens, Magic Circles, Malfatti Circles, McCay Circle, Midcircle, Monge's Theorem, Moser's Circle Problem, Neuberg Circles, Nine-Point Circle, Open Disk, P-Circle, Parry Circle, Pi, Polar Circle, Power (Circle), Prime Circle, Ptolemy's Theorem, Purser's Theorem, Radical Axis, Radius, Reuleaux Triangle, Seed of Life, Seifert Circle, Semicircle, Soddy Circles, Sphere, Taylor Circle, Triangle Inscribing in a Circle, Triplicate-Ratio Circle, Tucker Circles, Unit Circle, Venn Diagram, Villarceau Circles, Yin-Yang
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 125 and 197, 1987.
Casey, J. ``The Circle.'' Ch. 3 in
A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 96-150, 1893.
Courant, R. and Robbins, H.
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 74-75, 1996.
Dunham, W. ``Archimedes' Determination of Circular Area.'' Ch. 4 in
Journey Through Genius: The Great Theorems of Mathematics.
New York: Wiley, pp. 84-112, 1990.
Eppstein, D. ``Circles and Spheres.''
http://www.ics.uci.edu/~eppstein/junkyard/sphere.html.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 65-66, 1972.
MacTutor History of Mathematics Archive. ``Circle.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Circle.html.
Pappas, T. ``Infinity & the Circle'' and ``Japanese Calculus.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 68 and 139, 1989.
Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., 1995.
Yates, R. C. ``The Circle.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 21-25, 1952.
|
|
|
© 1996-9 Eric W. Weisstein