|
|
|
A plane is a 2-D Surface spanned by two linearly independent vectors. The generalization of the plane to higher Dimensions is called a Hyperplane.
In intercept form, a plane passing through the points ![]() ,
, ![]() and
and ![]() is given by
is given by
| (1) |
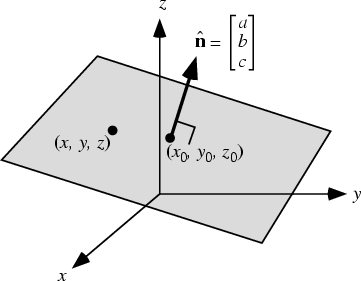
The equation of a plane Perpendicular to the Nonzero Vector
![]() through the point
through the point
![]() is
is
![\begin{displaymath}
\left[{\matrix{a\cr b\cr c\cr}}\right]\cdot \left[{\matrix{x...
... y-y_0\cr z-z_0\cr}}\right] = a(x-x_0)+ b(y-y_0)+c(z-z_0) = 0,
\end{displaymath}](p2_475.gif) |
(2) |
| (3) |
| (4) |
| (5) | |||
| (6) | |||
| (7) |
| (8) |
The plane through ![]() and parallel to
and parallel to
![]() and
and
![]() is
is
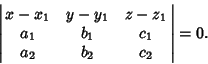 |
(9) |
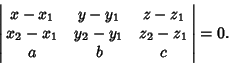 |
(10) |
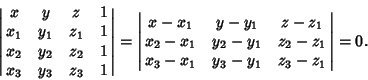 |
(11) |
The Distance from a point
![]() to a plane
to a plane
| (12) |
| (13) |
| (14) | |||
| (15) |
| (16) |
In order to specify the relative distances of ![]() points in the plane,
points in the plane,
![]() coordinates are needed, since the
first can always be placed at (0, 0) and the second at
coordinates are needed, since the
first can always be placed at (0, 0) and the second at ![]() , where it defines the x-Axis. The remaining
, where it defines the x-Axis. The remaining ![]() points need two coordinates each. However, the total number of distances is
points need two coordinates each. However, the total number of distances is
| (17) |
| (18) |
It is impossible to pick random variables which are uniformly distributed in the plane (Eisenberg and Sullivan 1996).
In 4-D, it is possible for four planes to intersect in exactly one point. For every set of ![]() points in the plane, there
exists a point
points in the plane, there
exists a point ![]() in the plane having the property such that every straight line through
in the plane having the property such that every straight line through ![]() has at least 1/3
of the points on each side of it (Honsberger 1985).
has at least 1/3
of the points on each side of it (Honsberger 1985).
Every Rigid motion of the plane is one of the following types (Singer 1995):
Every Rigid motion of the hyperbolic plane is one of the previous types or a
See also Argand Plane, Complex Plane, Dihedral Angle, Elliptic Plane, Fano Plane, Hyperplane, Moufang Plane, Nirenberg's Conjecture, Normal Section, Point-Plane Distance, Projective Plane
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 208-209, 1987.
Eisenberg, B. and Sullivan, R. ``Random Triangles
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 189-191, 1985.
Singer, D. A. ``Isometries of the Plane.'' Amer. Math. Monthly 102, 628-631, 1995.
Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity.
New York: Wiley, p. 7, 1972.
![]() Dimensions.'' Amer. Math. Monthly 103, 308-318, 1996.
Dimensions.'' Amer. Math. Monthly 103, 308-318, 1996.
|
|
|
© 1996-9 Eric W. Weisstein