|
|
|
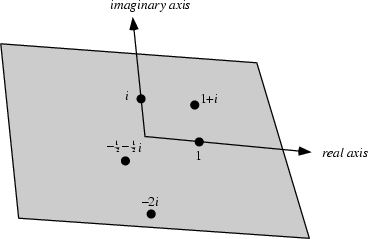
The plane of Complex Numbers spanned by the vectors 1 and ![]() , where
, where ![]() is the Imaginary
Number. Every Complex Number corresponds to a unique Point in the complex plane. The Line in the plane
with
is the Imaginary
Number. Every Complex Number corresponds to a unique Point in the complex plane. The Line in the plane
with ![]() is the Real Line. The complex plane is sometimes called the Argand Plane or Gauss Plane, and
a plot of Complex Numbers in the plane is sometimes called an Argand Diagram.
is the Real Line. The complex plane is sometimes called the Argand Plane or Gauss Plane, and
a plot of Complex Numbers in the plane is sometimes called an Argand Diagram.
See also Affine Complex Plane, Argand Diagram, Argand Plane, Bergman Space, Complex Projective Plane
References
Courant, R. and Robbins, H. ``The Geometric Interpretation of Complex Numbers.'' §5.2 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 92-97, 1996.