|
|
|
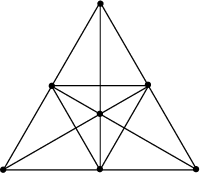
The 2-D Projective Plane over ![]() (``of order two''), illustrated above. It is a Block Design with
(``of order two''), illustrated above. It is a Block Design with ![]() ,
,
![]() ,
, ![]() ,
, ![]() , and
, and ![]() , and is also the Steiner Triple System
, and is also the Steiner Triple System ![]() .
.
The Fano plane also solves the Transylvania Lottery, which picks three numbers from the Integers
1-14. Using two Fano planes we can guarantee matching two by playing just 14 times as follows. Label the
Vertices of one Fano plane by the Integers 1-7, the other plane by the
Integers 8-14. The 14 tickets to play are the 14 lines of the two planes. Then if ![]() is the
winning ticket, at least two of
is the
winning ticket, at least two of ![]() are either in the interval [1, 7] or [8, 14]. These two numbers are on exactly one
line of the corresponding plane, so one of our tickets matches them.
are either in the interval [1, 7] or [8, 14]. These two numbers are on exactly one
line of the corresponding plane, so one of our tickets matches them.
The Lehmers (1974) found an application of the Fano plane for factoring Integers via Quadratic Forms. Here, the triples of forms used form the lines of the Projective Geometry on seven points, whose planes are Fano configurations corresponding to pairs of residue classes mod 24 (Lehmer and Lehmer 1974, Guy 1975, Shanks 1985). The group of Automorphisms (incidence-preserving Bijections) of the Fano plane is the Simple Group of Order 168 (Klein 1870).
See also Design, Projective Plane, Steiner Triple System, Transylvania Lottery
References
Guy, R. ``How to Factor a Number.'' Proc. Fifth Manitoba Conf. on Numerical Math., 49-89, 1975.
Lehmer, D. H. and Lehmer, E. ``A New Factorization Technique Using Quadratic Forms.'' Math. Comput. 28, 625-635, 1974.
Shanks, D. Solved and Unsolved Problems in Number Theory, 3rd ed. New York: Chelsea, pp. 202 and 238, 1985.