Let 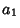 ,
, 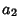 , ...,
, ..., 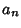 be Scalars not all equal to 0. Then the Set
be Scalars not all equal to 0. Then the Set 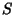 consisting of
all Vectors
consisting of
all Vectors
in  such that
such that
is a Subspace of  called a hyperplane. More generally, a hyperplane is any co-dimension 1 vector
Subspace of a Vector Space. Equivalently, a hyperplane
called a hyperplane. More generally, a hyperplane is any co-dimension 1 vector
Subspace of a Vector Space. Equivalently, a hyperplane 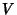 in a Vector Space
in a Vector Space 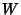 is any
Subspace such that
is any
Subspace such that 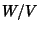 is 1-dimensional. Equivalently, a hyperplane is the Kernel of any Nonzero linear Map from the Vector Space to the underlying Field.
is 1-dimensional. Equivalently, a hyperplane is the Kernel of any Nonzero linear Map from the Vector Space to the underlying Field.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ,
, ![]() , ...,
, ..., ![]() be Scalars not all equal to 0. Then the Set
be Scalars not all equal to 0. Then the Set ![]() consisting of
all Vectors
consisting of
all Vectors
![\begin{displaymath}
{\bf X} = \left[{\matrix{x_1\cr x_2\cr \vdots\cr x_n\cr}}\right]
\end{displaymath}](h_2374.gif)