|
|
|
Let ![]() be a Real Vector Space (e.g., the real continuous functions
be a Real Vector Space (e.g., the real continuous functions ![]() on a
Closed Interval
on a
Closed Interval ![]() , 2-D Euclidean Space
, 2-D Euclidean Space ![]() , the twice differentiable real functions
, the twice differentiable real functions ![]() on
on
![]() , etc.). Then
, etc.). Then ![]() is a real Subspace of
is a real Subspace of ![]() if
if ![]() is a Subset of
is a Subset of ![]() and, for every
and, for every
![]() ,
,
![]() and
and ![]() (the Reals),
(the Reals),
![]() and
and
![]() . Let
. Let ![]() be a homogeneous system of linear equations in
be a homogeneous system of linear equations in ![]() , ...,
, ..., ![]() . Then the
Subset
. Then the
Subset ![]() of
of ![]() which consists of all solutions of the system
which consists of all solutions of the system ![]() is a subspace of
is a subspace of ![]() .
.
More generally, let ![]() be a Field with
be a Field with ![]() , where
, where ![]() is Prime, and let
is Prime, and let ![]() denote the
denote the ![]() -D
Vector Space over
-D
Vector Space over ![]() . The number of
. The number of ![]() -D linear subspaces of
-D linear subspaces of ![]() is
is
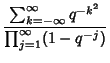 |
|||
 |
See also q-Binomial Coefficient, Subfield, Submanifold
References
Aigner, M. Combinatorial Theory. New York: Springer-Verlag, 1979.
Exton, H.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/dig/dig.html
![]() -Hypergeometric Functions and Applications. New York: Halstead Press, 1983.
-Hypergeometric Functions and Applications. New York: Halstead Press, 1983.