Quadrilateral

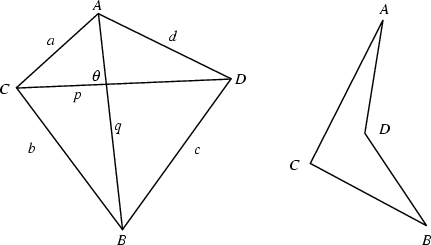
A four-sided Polygon sometimes (but not very often) also known as a Tetragon. If not explicitly stated, all four Vertices are generally taken to lie in a Plane. If the points do not lie in a Plane, the quadrilateral is called a Skew Quadrilateral.

For a planar convex quadrilateral (left figure above), let the lengths of the sides be $a$, $b$, $c$, and $d$, the Semiperimeter $s$, and the Diagonals $p$ and $q$. The Diagonals are Perpendicular Iff $a^2+c^2=b^2+d^2$. An equation for the sum of the squares of side lengths is

$$a^2+b^2+c^2+d^2=p^2+q^2+4x^2,$$ (1)

where $x$ is the length of the line joining the Midpoints of the Diagonals. The Area of a quadrilateral is given by

$$K = {\textstyle{1\over 2}}pq\sin\theta$$ (2)

$$= {\textstyle{1\over 4}}(b^2+d^2-a^2-c^2)\tan\theta$$ (3)

$$= {\textstyle{1\over 4}}\sqrt{4p^2q^2-(b^2+d^2-a^2-c^2)^2}$$ (4)

$$= \sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2[{\textstyle{1\over 2}}(A+B)]},$$ (5)

where (4) is known as Bretschneider's Formula (Beyer 1987).

A special type of quadrilateral is the Cyclic Quadrilateral, for which a Circle can be circumscribed so that it touches each Vertex. For Bicentric quadrilaterals, the Circumcircle and Incircle satisfy

$$2r^2(R^2-s^2)=(R^2-s^2)^2-4r^2s^2,$$ (6)

where $R$ is the Circumradius, $r$ in the Inradius, and $s$ is the separation of centers. A quadrilateral with two sides Parallel is called a Trapezoid.

There is a relationship between the six distances $d_{12}$, $d_{13}$, $d_{14}$, $d_{23}$, $d_{24}$, and $d_{34}$ between the four points of a quadrilateral (Weinberg 1972):

$$0 = d_{12}^4 d_{34}^2+d_{13}^4 d_{24}^2+d_{14}^4 d_{23}^2+d_{23}^4 d_{14}^2+d_{24}^4 d_{13}^2+d_{34}^4 d_{12}^2$$

$$\phantom{=} +d_{12}^2d_{23}^2d_{31}^2+d_{12}^2d_{24}^2d_{41}^2+d_{13}^2d_{34}^2d_{41}^2$$

$$\phantom{=} +d_{23}^2d_{34}^2d_{42}^2-d_{12}^2d_{23}^2d_{34}^2-d_{13}^2d_{32}^2d_{24}^2$$

$$\phantom{=} -d_{12}^2d_{24}^2d_{43}^2-d_{14}^2d_{42}^2d_{23}^2-d_{13}^2d_{34}^2d_{42}^2$$

$$\phantom{=} -d_{14}^2d_{43}^2d_{32}^2-d_{23}^2d_{31}^2d_{14}^2-d_{21}^2d_{13}^2d_{34}^2$$

$$\phantom{=} -d_{24}^2d_{41}^2d_{13}^2-d_{21}^2d_{14}^2d_{43}^2-d_{31}^2d_{12}^2d_{24}^2$$

$$\phantom{=} -d_{32}^2d_{21}^2d_{14}^2.$$ (7)

See also Bimedian, Brahmagupta's Formula, Bretschneider's Formula, Complete Quadrilateral, Cyclic-Inscriptable Quadrilateral, Cyclic Quadrilateral, Diamond, Eight-Point Circle Theorem, Equilic Quadrilateral, Fano's Axiom, Léon Anne's Theorem, Lozenge, Orthocentric Quadrilateral, Parallelogram, Ptolemy's Theorem, Rational Quadrilateral, Rhombus, Skew Quadrilateral, Trapezoid, Varignon's Theorem, von Aubel's Theorem, Wittenbauer's Parallelogram

References

Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 123, 1987.

Routh, E. J. ``Moment of Inertia of a Quadrilateral.'' Quart. J. Pure Appl. Math. 11, 109-110, 1871.

Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York: Wiley, p. 7, 1972.